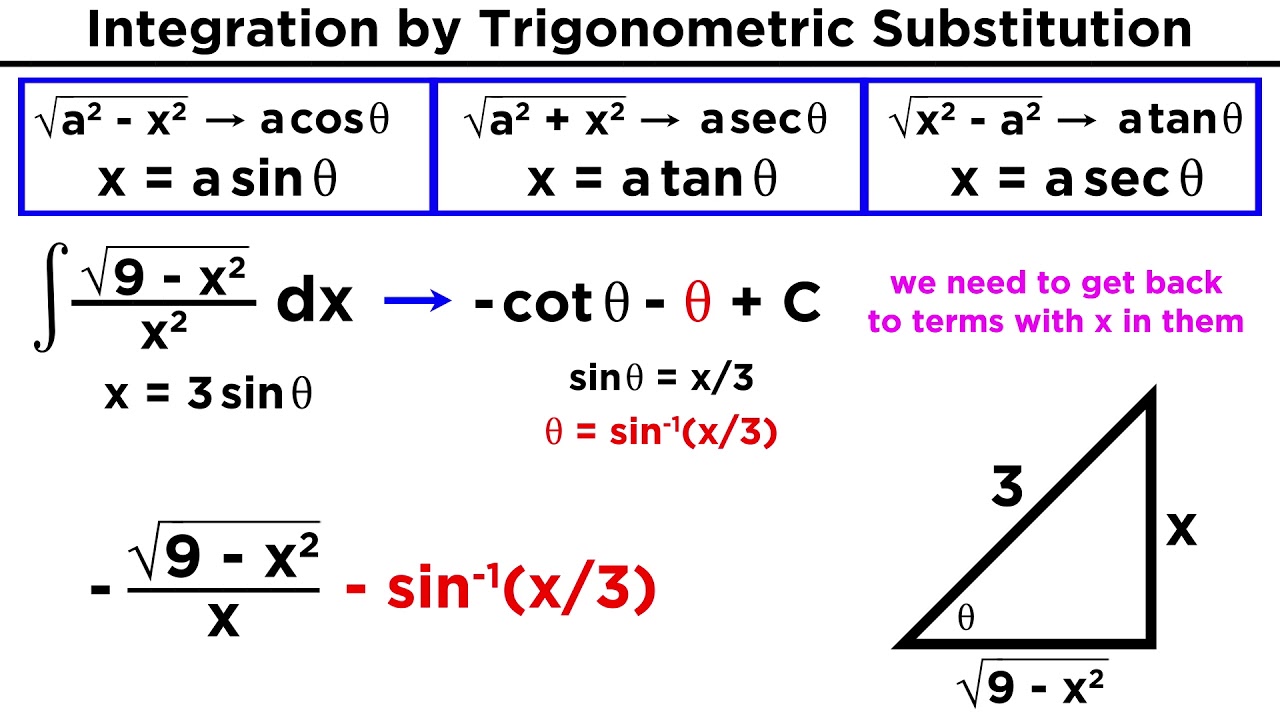
Integration By Trigonometric Substitution Step By Step Explanation In this calculus video tutorial, we evaluate three integrals using the three trigonometric substitution equations x=a*sin\\theta, a*tan\\theta, and a*sec\\theta. Figure 7.3.7: calculating the area of the shaded region requires evaluating an integral with a trigonometric substitution. we can see that the area is a = ∫5 3√x2 − 9dx. to evaluate this definite integral, substitute x = 3secθ and dx = 3secθtanθdθ. we must also change the limits of integration.
Integration By Trigonometric Substitution Youtube Example 6.4.6: using trigonometric substitution. evaluate ∫ 1 (x2 6x 10)2 dx. solution. we start by completing the square, then make the substitution u = x 3, followed by the trigonometric substitution of u = tanθ: ∫ 1 (x2 6x 10)2 dx = ∫ 1 ((x 3)2 1)2 dx = ∫ 1 (u2 1)2 du. now make the substitution u = tanθ, du = sec2θ. Integrate using trigo substitution int dx (sqrt (x^2 4x))^3 ? by changing variables, integration can be simplified by using the substitutions x=a\sin (\theta), x=a\tan (\theta), or x=a\sec (\theta). once the substitution is made the function can be simplified using basic trigonometric identities. The trigonometric identity we shall use here is one of the ‘double angle’ formulae: cos 2a = 1 − 2 sin2 a. by rearranging this we can write. sin2 a =. (1 − cos 2a) notice that by using this identity we can convert an expression involving sin2 has no powers in. therefore, our integral can be written. into one which. Exercise 7.2.2. evaluate ∫cos3xsin2xdx. hint. answer. in the next example, we see the strategy that must be applied when there are only even powers of sinx and cosx. for integrals of this type, the identities. sin2x = 1 2 − 1 2cos(2x) = 1 − cos(2x) 2. and. cos2x = 1 2 1 2cos(2x) = 1 cos(2x) 2.
Trigonometric Substitution 6 Integral Calculus Youtube The trigonometric identity we shall use here is one of the ‘double angle’ formulae: cos 2a = 1 − 2 sin2 a. by rearranging this we can write. sin2 a =. (1 − cos 2a) notice that by using this identity we can convert an expression involving sin2 has no powers in. therefore, our integral can be written. into one which. Exercise 7.2.2. evaluate ∫cos3xsin2xdx. hint. answer. in the next example, we see the strategy that must be applied when there are only even powers of sinx and cosx. for integrals of this type, the identities. sin2x = 1 2 − 1 2cos(2x) = 1 − cos(2x) 2. and. cos2x = 1 2 1 2cos(2x) = 1 cos(2x) 2. When our integral is set up like that, we can do this substitution: then we can integrate f (u), and finish by putting g (x) back as u. like this: example: ∫ cos (x 2) 2x dx. we know (from above) that it is in the right form to do the substitution: now integrate: ∫ cos (u) du = sin (u) c. Identify that it’s a trig sub problem. 28:18 step 2. decide which trig substitution to use. 28:46 step 3. do the setup process for trig sub. 30:03 step 4. make substitutions into the integral. 31:18 step 5. simplify the integral using whatever methods you need to, then integrate.
Integration Formulas For Trig Substitution Youtube When our integral is set up like that, we can do this substitution: then we can integrate f (u), and finish by putting g (x) back as u. like this: example: ∫ cos (x 2) 2x dx. we know (from above) that it is in the right form to do the substitution: now integrate: ∫ cos (u) du = sin (u) c. Identify that it’s a trig sub problem. 28:18 step 2. decide which trig substitution to use. 28:46 step 3. do the setup process for trig sub. 30:03 step 4. make substitutions into the integral. 31:18 step 5. simplify the integral using whatever methods you need to, then integrate.
Integration By Trigonometric Substitution Youtube
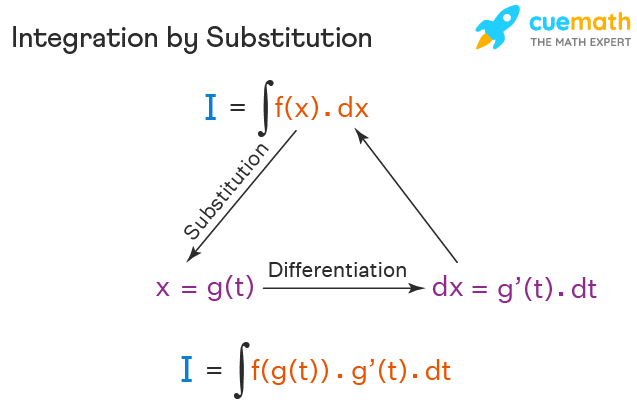
Integration By Substitution Definition Formula Methods Examples
Comments are closed.