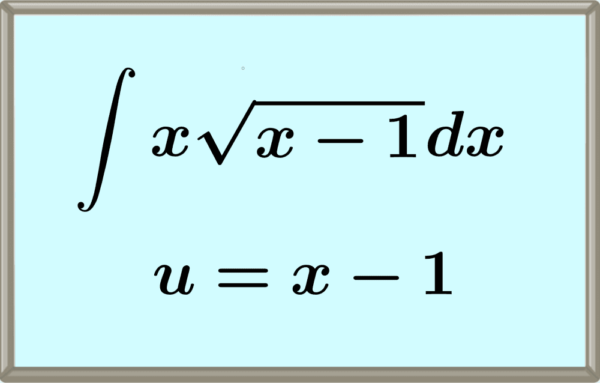
Integration By Substitution Examples With Answers Neurochispas 1. find a substitution that simplifies the integral. this means finding a new variable, say u u, that is a function of x x and has a derivative that is easy to integrate. 2. substitute the new variable, u, into the original integral. we will obtain an integral of the form \int g (u)du ∫ g(u)du. To integrate functions using this method, we follow the steps below: 1. choose two functions, u and dv dx. the product of the two functions, u\frac {dv} {dx} udxdv is the integrand. 2. determine the derivative of u with respect to x and call it u ′. 3. determine the integral of dv dx with respect to x and call it v. 4.
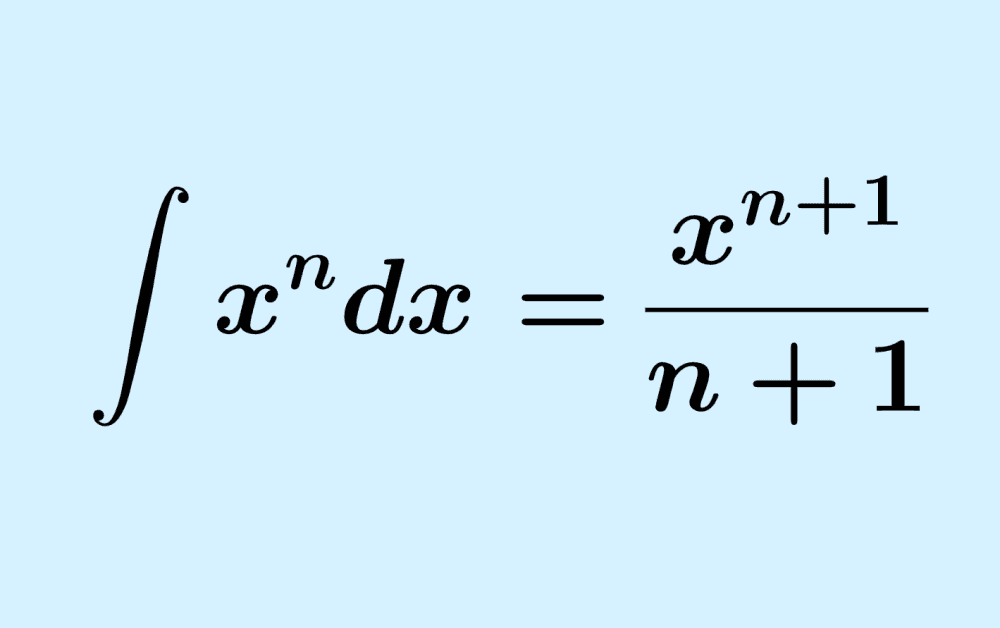
Integrals Of Polynomials Examples With Answers Neurochispas The chain rule for integrals is an integration rule related to the chain rule for derivatives. this rule is used for integrating functions of the form f'(x)[f(x)] n. here, we will learn how to find integrals of functions using the chain rule for integrals. then we will look at some examples where we will apply this rule. Example 4.1.1: integrating by substitution. evaluate ∫ xsin(x2 5) dx. solution. knowing that substitution is related to the chain rule, we choose to let u be the "inside" function of sin(x2 5). (this is not always a good choice, but it is often the best place to start.) let u = x2 5, hence du = 2xdx. When our integral is set up like that, we can do this substitution: then we can integrate f (u), and finish by putting g (x) back as u. like this: example: ∫ cos (x 2) 2x dx. we know (from above) that it is in the right form to do the substitution: now integrate: ∫ cos (u) du = sin (u) c. Guidelines for integration by substitution. 1. let u be a function of x (usually part of the integrand). 2. solve for x and dx in terms of u and du. 3. convert the entire integral to u variable form and try to fit it to one or more of the basic integration formulas. if none fits, try a different substitution.
Integration By Substitution Examples With Explanation And Pdf When our integral is set up like that, we can do this substitution: then we can integrate f (u), and finish by putting g (x) back as u. like this: example: ∫ cos (x 2) 2x dx. we know (from above) that it is in the right form to do the substitution: now integrate: ∫ cos (u) du = sin (u) c. Guidelines for integration by substitution. 1. let u be a function of x (usually part of the integrand). 2. solve for x and dx in terms of u and du. 3. convert the entire integral to u variable form and try to fit it to one or more of the basic integration formulas. if none fits, try a different substitution. Integration by parts to reverse the chain rule we have the method of u substitution. to reverse the product rule we also have a method, called integration by parts. the formula is given by: theorem (integration by parts formula) ˆ f(x)g(x)dx = f(x)g(x) − ˆ f(x)g′(x)dx where f(x) is an anti derivative of f(x). By substitution. carry out the following integrations by substitution only. carry out the following integrations by substitution only. carry out the following integrations by substitution only. 4 3 ) c. 6 5 x ) c. only. only. carry out the following integrations.
Comments are closed.