Integration By Substitution Definition Formula Methods Examples

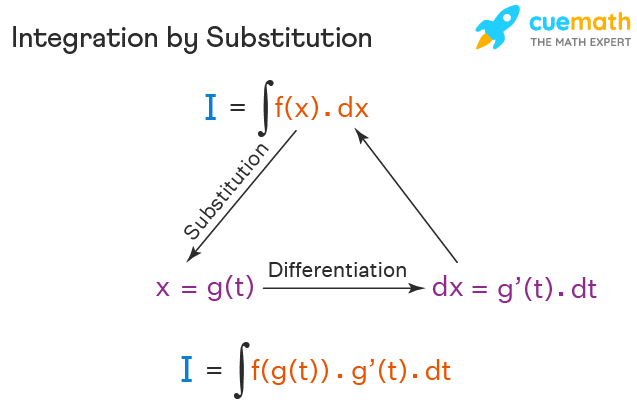
Integration By Substitution Definition Formula Methods Examples "integration by substitution" (also called "u substitution" or "the reverse chain rule") is a method to find an integral, but only when it can be set up in a special way. the first and most vital step is to be able to write our integral in this form: note that we have g(x) and its derivative g'(x) like in this example:. The following are the steps that are helpful in performing this method of integration by substitution. step 1: choose a new variable t for the given function to be reduced. step 2: determine the value of dx, of the given integral, where f (x) is integrated with respect to x. step 3: make the required substitution in the function f (x.

Ppt Integration By Substitution Powerpoint Presentation Free Example 4.1.1: integrating by substitution. evaluate ∫ xsin(x2 5) dx. solution. knowing that substitution is related to the chain rule, we choose to let u be the "inside" function of sin(x2 5). (this is not always a good choice, but it is often the best place to start.) let u = x2 5, hence du = 2xdx. Let u = cos(θ) u = cos (θ) and take differentials of both sides. substitute these into the integral and see if you can simplify. theorem: substitution method for indefinite integrals. if u = g(x) is a differentiable function whose range is an interval i and f is continuous on i, then. ∫f(g(x))g′(x)dx = ∫f(u)du. In calculus, the integration by substitution method is also known as the “reverse chain rule” or “u substitution method”. we can use this method to find an integral value when it is set up in the special form. it means that the given integral is of the form: ∫ f (g (x)).g' (x).dx = f (u).du. 1. find a substitution that simplifies the integral. this means finding a new variable, say u u, that is a function of x x and has a derivative that is easy to integrate. 2. substitute the new variable, u, into the original integral. we will obtain an integral of the form \int g (u)du ∫ g(u)du.

Ppt Integration By Substitution Powerpoint Presentation Free In calculus, the integration by substitution method is also known as the “reverse chain rule” or “u substitution method”. we can use this method to find an integral value when it is set up in the special form. it means that the given integral is of the form: ∫ f (g (x)).g' (x).dx = f (u).du. 1. find a substitution that simplifies the integral. this means finding a new variable, say u u, that is a function of x x and has a derivative that is easy to integrate. 2. substitute the new variable, u, into the original integral. we will obtain an integral of the form \int g (u)du ∫ g(u)du. Example 4.3.1. determine the general antiderivative of. h(x) = (5x − 3)6. check the result by differentiating. for this composite function, the outer function f is f(u) = u6, while the inner function is u(x) = 5x − 3. since the antiderivative of f is f(u) = 1 7u7 c, we see that the antiderivative of h is. Calculus. in calculus, integration by substitution, also known as u substitution, reverse chain rule or change of variables, [1] is a method for evaluating integrals and antiderivatives. it is the counterpart to the chain rule for differentiation, and can loosely be thought of as using the chain rule "backwards.".