Inscribed Angles Of A Circle Theorem
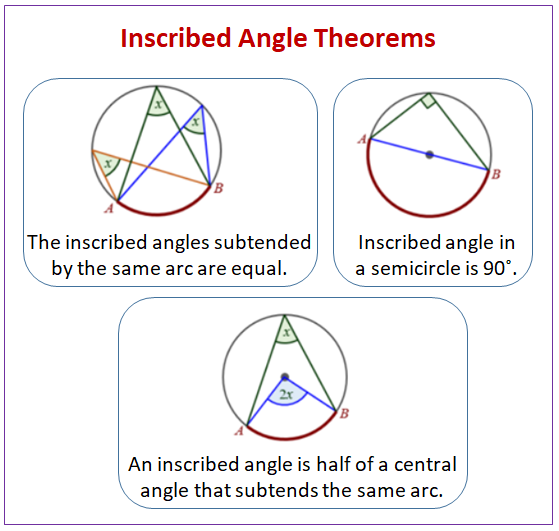
Circle Theorems Inscribed Angle Theorem Video Lessons Examples Learn the inscribed angle theorem, which states that an inscribed angle is half of a central angle that subtends the same arc. see the proof, properties, and examples of this theorem with diagrams and worksheets. Learn about inscribed angles, central angles, and how to use them to find circle properties. explore examples, interactive diagrams, and proofs of theorems related to circles.
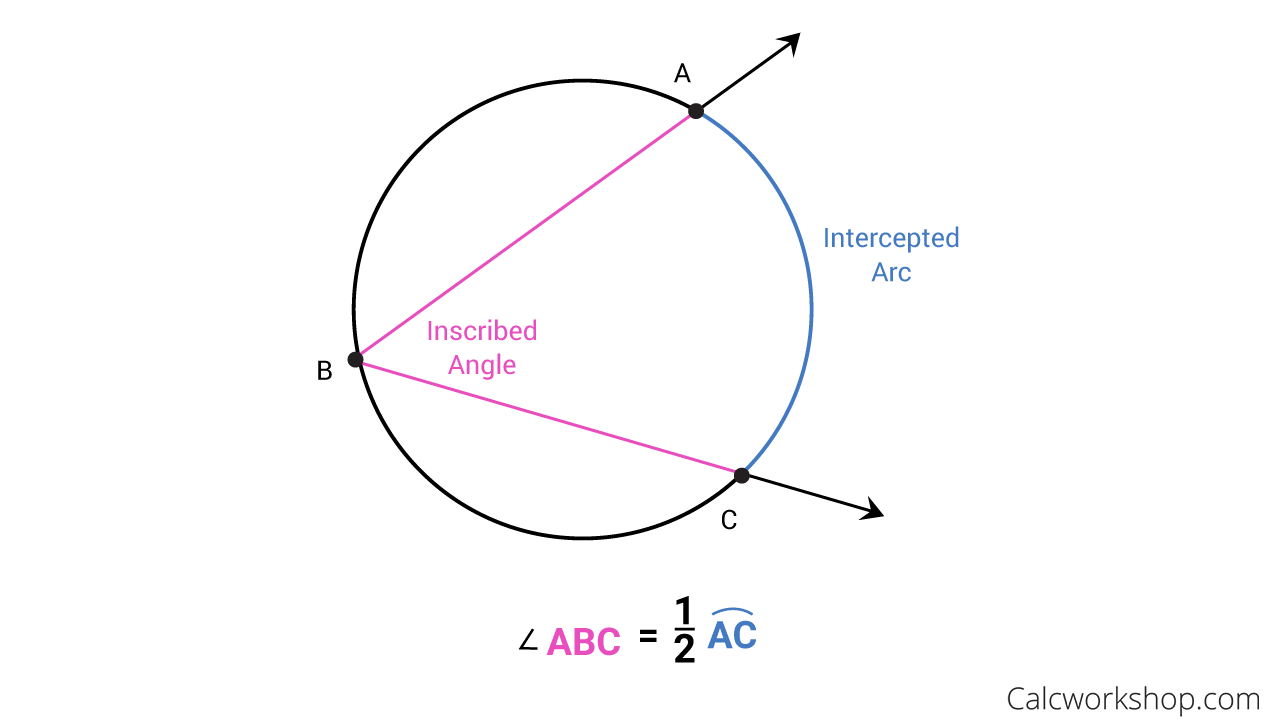
Inscribed Angle Everything You Need To Know 2019 According to the inscribed angle theorem, the measure of the inscribed angle is half the measure of the central angle, ∠abc = 2∠cda. hence, ∠abc =2 x 20° = 40°. now, (4x 20)° = 40°. 4x = 40° 20°. x =20° 4 = 5°. what is an inscribed angle of a circle and how to find their measure– its definition in geometry with formula, proof. The angle at the centre of a circle is twice any angle at the circumference subtended by the same arc. the following diagrams illustrates the inscribed angle theorem. example: the center of the following circle is o. bod is a diameter of the circle. find the value of x. solution: ∠boc 70˚ = 180˚. Supplementary inscribed angle θ on minor arc. in geometry, an inscribed angle is the angle formed in the interior of a circle when two chords intersect on the circle. it can also be defined as the angle subtended at a point on the circle by two given points on the circle. equivalently, an inscribed angle is defined by two chords of the circle. We've shown that a case 3 inscribed angle intercepts an arc with twice the measure of the angle—same as a case 1 angle or a case 2 angle. since any inscribed angle falls into one of the three cases, we've proven the inscribed angle theorem : for ∠ abc inscribed in a circle containing points a and c , m ac = 2 × m∠ abc .
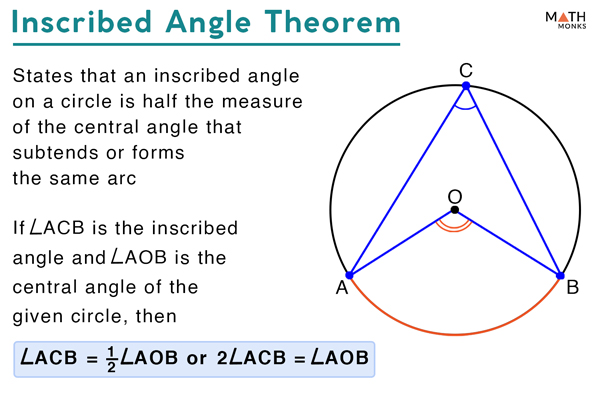
Inscribed Angle Definition Formula Theorem With Examples Supplementary inscribed angle θ on minor arc. in geometry, an inscribed angle is the angle formed in the interior of a circle when two chords intersect on the circle. it can also be defined as the angle subtended at a point on the circle by two given points on the circle. equivalently, an inscribed angle is defined by two chords of the circle. We've shown that a case 3 inscribed angle intercepts an arc with twice the measure of the angle—same as a case 1 angle or a case 2 angle. since any inscribed angle falls into one of the three cases, we've proven the inscribed angle theorem : for ∠ abc inscribed in a circle containing points a and c , m ac = 2 × m∠ abc . See central angle definition the central angle is always twice the inscribed angle. see central angle theorem. relationship to thales' theorem. refer to the above figure. if the two points a,b form a diameter of the circle, the inscribed angle will be 90°, which is thales' theorem. you can verify this yourself by solving the formula above. Inscribed angle theorem proof. inscribed shapes: angle subtended by diameter. inscribed shapes: find inscribed angle. angle measurement & circle arcs. angles in circles. angles in circles word problems. proof: radius is perpendicular to tangent line. determining tangent lines: angles. proof: perpendicular radius bisects chord.

Comments are closed.