Inscribed Angles Lesson Math Geometry Showme

Inscribed Angles Lesson Math Geometry Showme Inscribed angles lesson by angela knipple april 10, 2013. math; geometry; like 0. you should do so only if this showme contains inappropriate content. Lesson 10 4 inscribed angles by lisa hastings smith april 27, 2016.

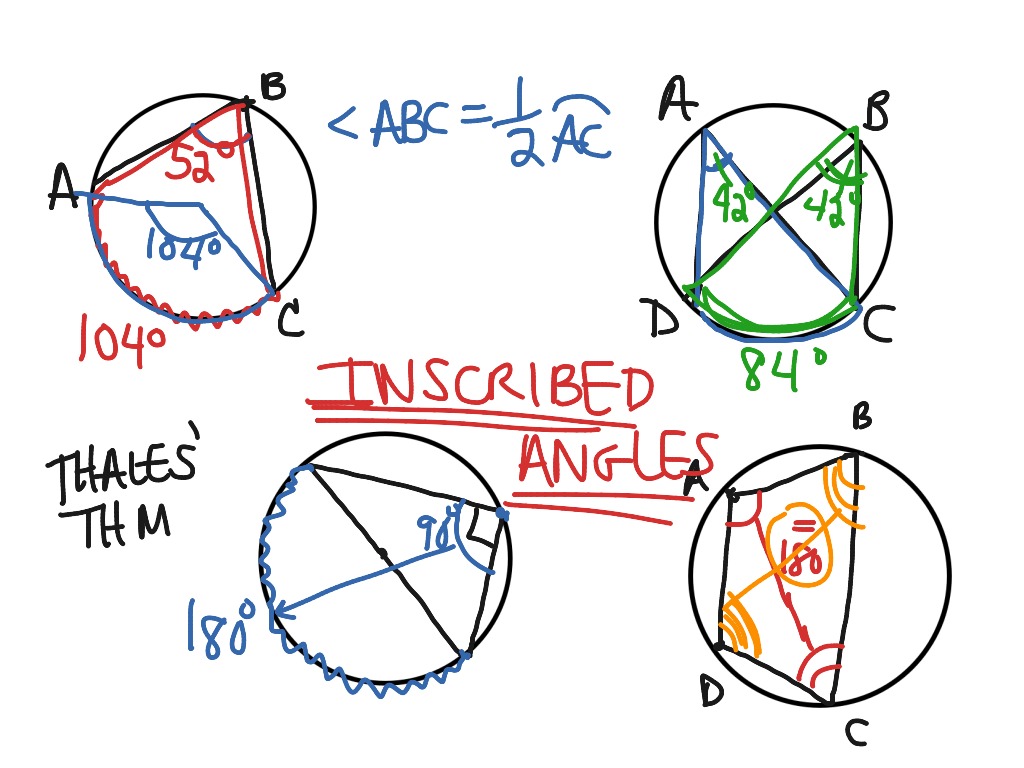
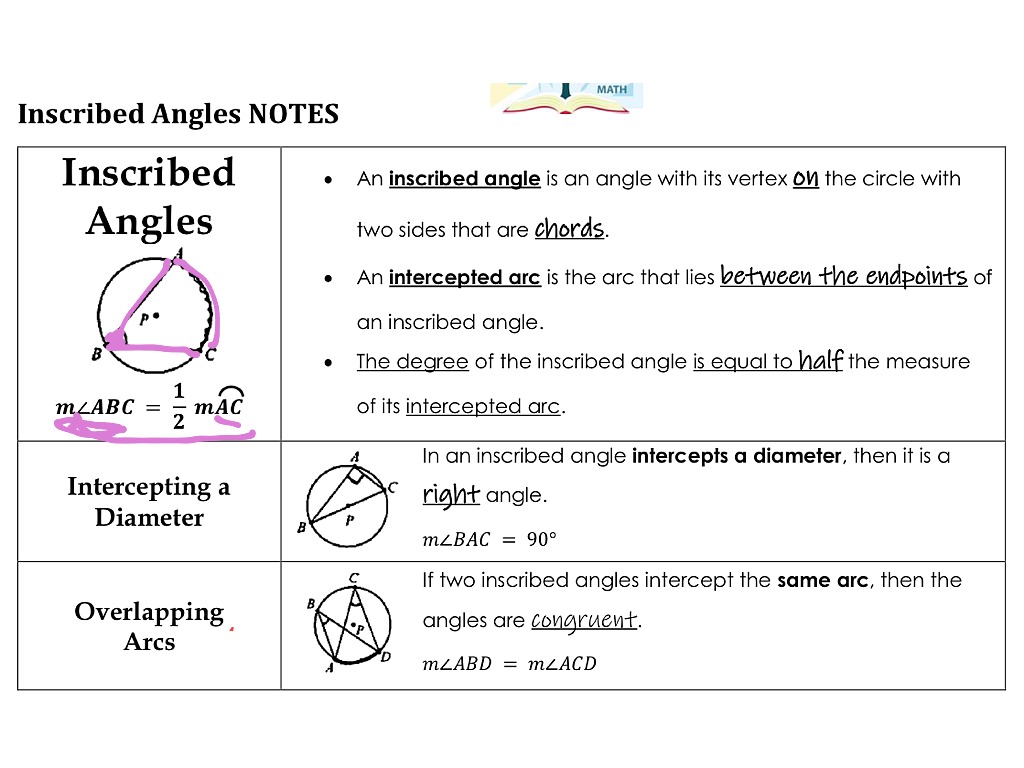
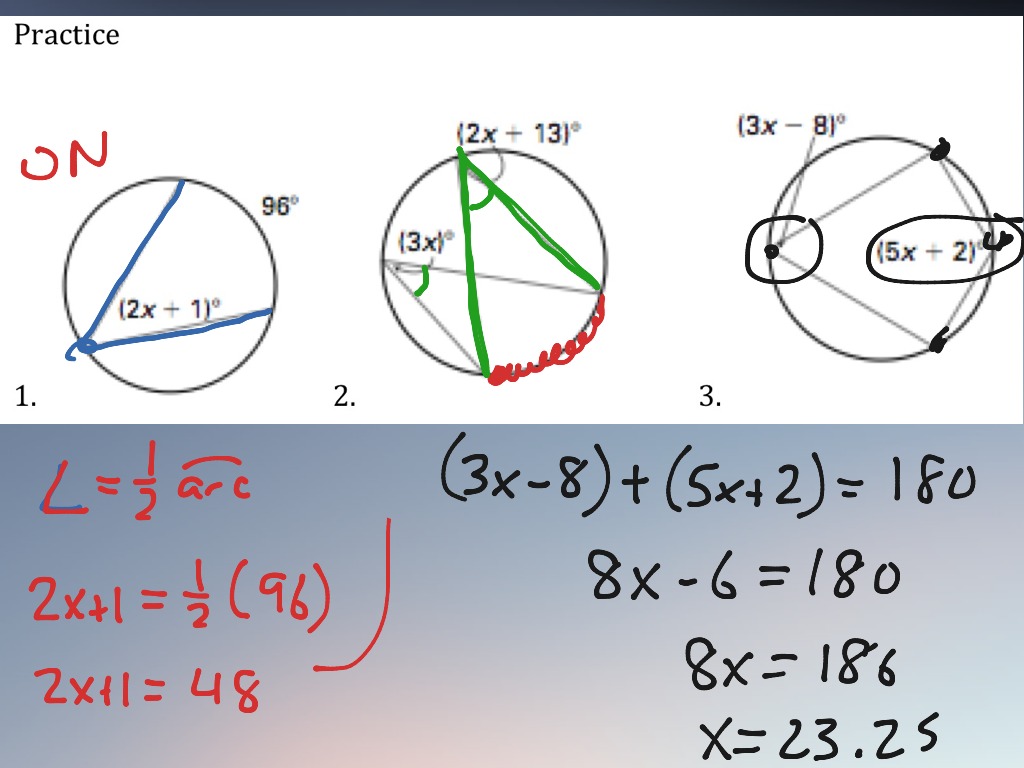
Lesson 10 4 Inscribed Angles Math Geometry Circles Showme High school geometry. course: high school geometry > unit 8. lesson 7: inscribed angles. inscribed angles. inscribed angles. challenge problems: inscribed angles. inscribed angle theorem proof. inscribed angle theorem proof. For the circle at right with center c, ∠acb is a central angle. an inscribed angle is an angle with its vertex on the circle and whose sides intersect the circle. the arc formed by the intersection of the two sides of the angle and the circle is called an intercepted arc. ∠adb is an inscribed angle, ab!is an intercepted arc. Inscribed angle. intercepted arc inscribed angle a b c 12 3 11 finding the measure of an inscribed angle hands on activity: exploring inscribed angles • draw two large circles with a compass. label the centers x and y. • on the circles, use a straightedge and copy the diagrams shown. 1. a. patterns in x, use a protractor to measure &axb and. Angle = (11 × 360°) (2 × 22 7 × 7) angle = 90°. therefore, the angle of the arc is 90°. example 2: find the missing angle x in the diagram below. solution: we need to find the value of x. one angle is given as 80°. by inscribed angle theorem we know that the central angle = 2 × inscribed angle. x = 2 × 80.

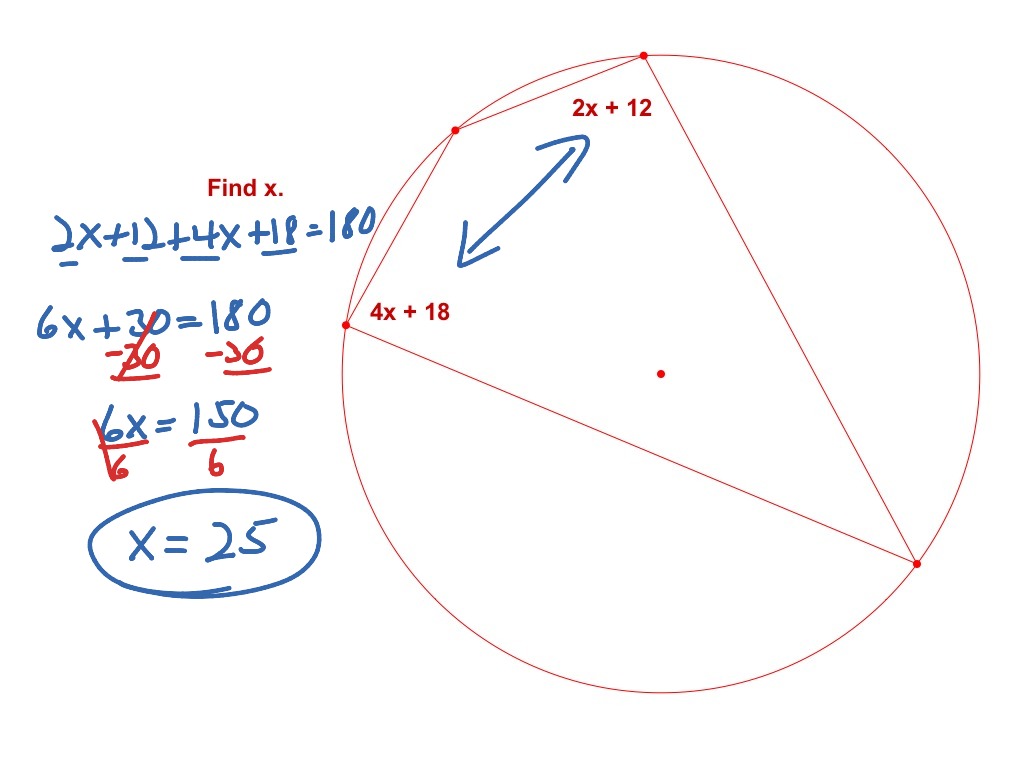
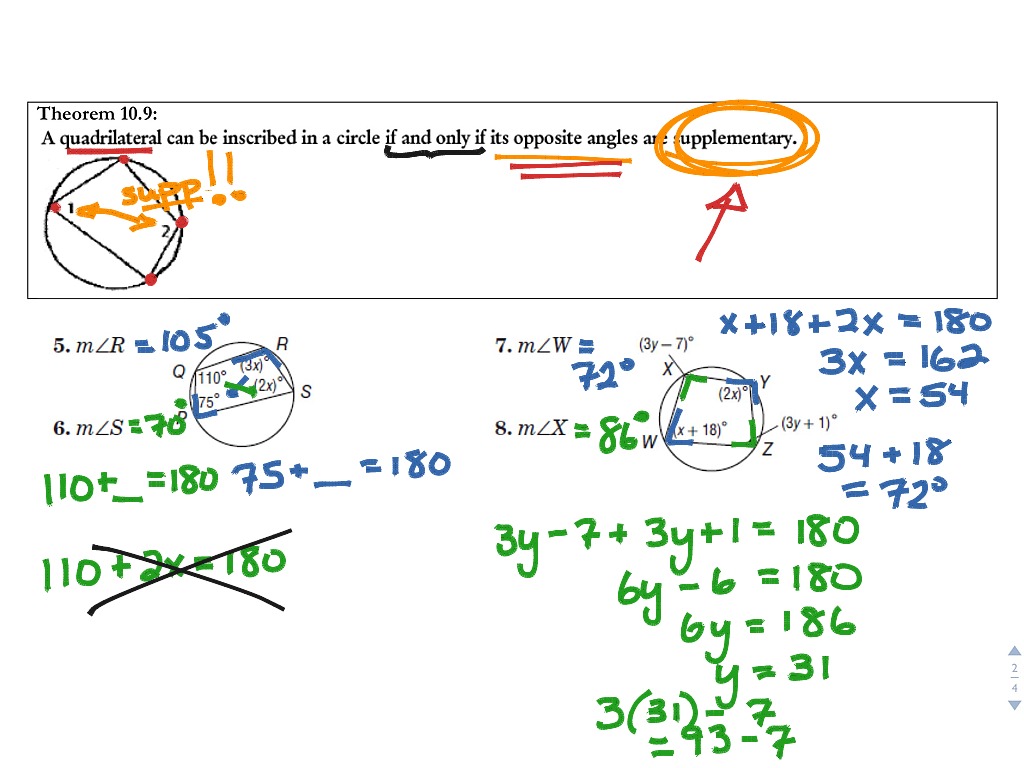
Inscribed Angles Math Geometry Circles Showme Inscribed angle. intercepted arc inscribed angle a b c 12 3 11 finding the measure of an inscribed angle hands on activity: exploring inscribed angles • draw two large circles with a compass. label the centers x and y. • on the circles, use a straightedge and copy the diagrams shown. 1. a. patterns in x, use a protractor to measure &axb and. Angle = (11 × 360°) (2 × 22 7 × 7) angle = 90°. therefore, the angle of the arc is 90°. example 2: find the missing angle x in the diagram below. solution: we need to find the value of x. one angle is given as 80°. by inscribed angle theorem we know that the central angle = 2 × inscribed angle. x = 2 × 80. Now, we will investigation the relationship between the inscribed angle, the central angle and the arc they intercept. investigation 9 4: measuring an inscribed angle tools needed: pencil, paper, compass, ruler, protractor 1. draw three circles with three different inscribed angles. for j a, make one side of the inscribed angle a diameter, for j. According to the inscribed angle theorem, the measure of the inscribed angle is half the measure of the central angle, ∠abc = 2∠cda. hence, ∠abc =2 x 20° = 40°. now, (4x 20)° = 40°. 4x = 40° 20°. x =20° 4 = 5°. what is an inscribed angle of a circle and how to find their measure– its definition in geometry with formula, proof.

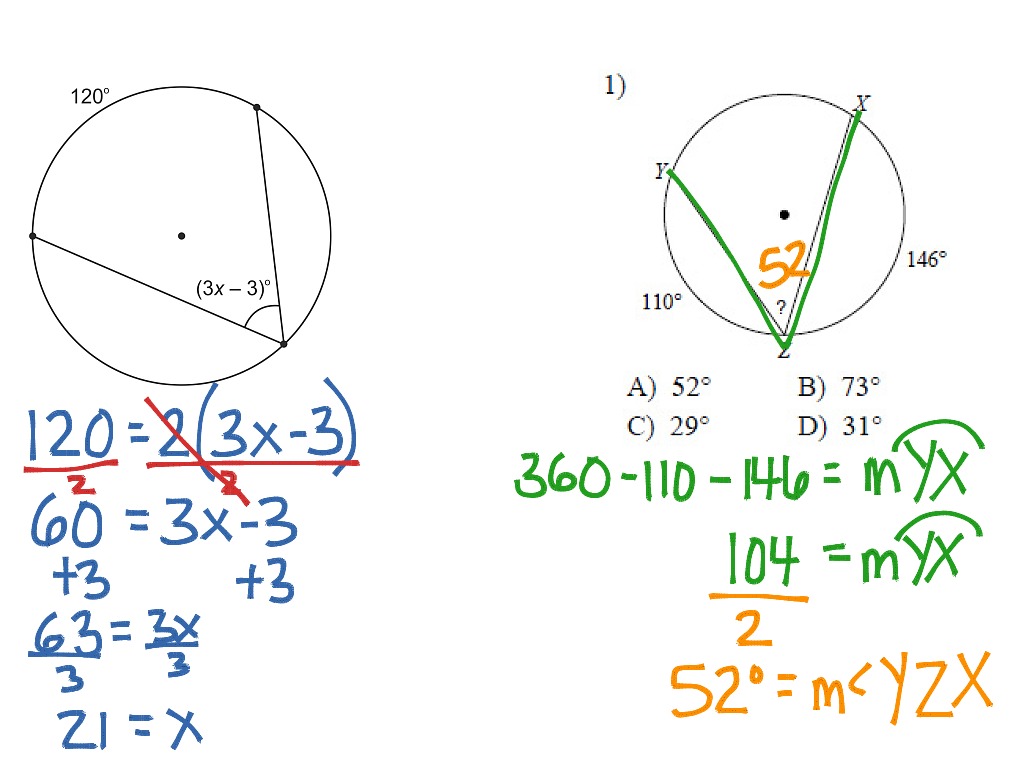
Inscribed Angles Circles Inscribed Angles Math Showme Now, we will investigation the relationship between the inscribed angle, the central angle and the arc they intercept. investigation 9 4: measuring an inscribed angle tools needed: pencil, paper, compass, ruler, protractor 1. draw three circles with three different inscribed angles. for j a, make one side of the inscribed angle a diameter, for j. According to the inscribed angle theorem, the measure of the inscribed angle is half the measure of the central angle, ∠abc = 2∠cda. hence, ∠abc =2 x 20° = 40°. now, (4x 20)° = 40°. 4x = 40° 20°. x =20° 4 = 5°. what is an inscribed angle of a circle and how to find their measure– its definition in geometry with formula, proof.

Inscribed Angles Math High School Math Geometry Models Geometry

Geom 10 3 Inscribed Angles B Math Geometry Inscribed Angles Showme