Inscribed Angle Theorem Circles Proof And Examples
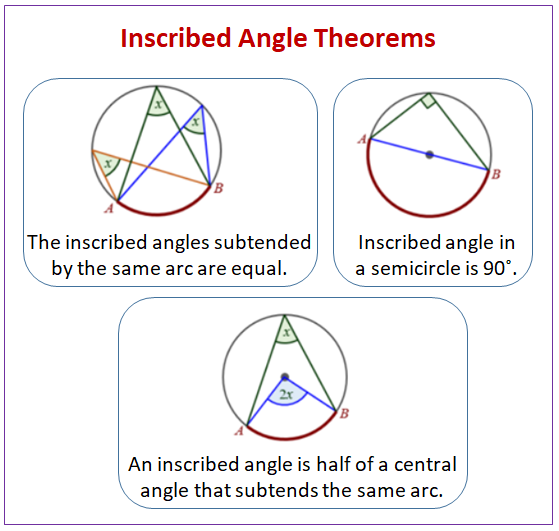
Circle Theorems Inscribed Angle Theorem Video Lessons Examples Example 2: find the missing angle x in the diagram below. solution: we need to find the value of x. one angle is given as 80°. by inscribed angle theorem we know that the central angle = 2 × inscribed angle. x = 2 × 80. x = 160. therefore, the value of x = 160°. become a problem solving champ using logic, not rules. Angle measurement & circle arcs. angles in circles. angles in circles word problems. proof: radius is perpendicular to tangent line. determining tangent lines: angles. proof: perpendicular radius bisects chord. proof: radius is perpendicular to a chord it bisects. tangents of circles problem (example 1) tangents of circles problem (example 2).
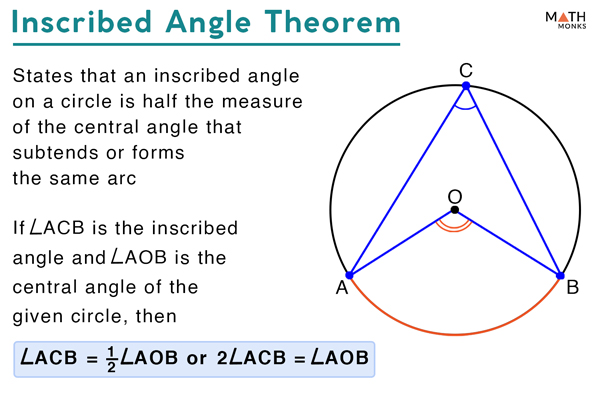
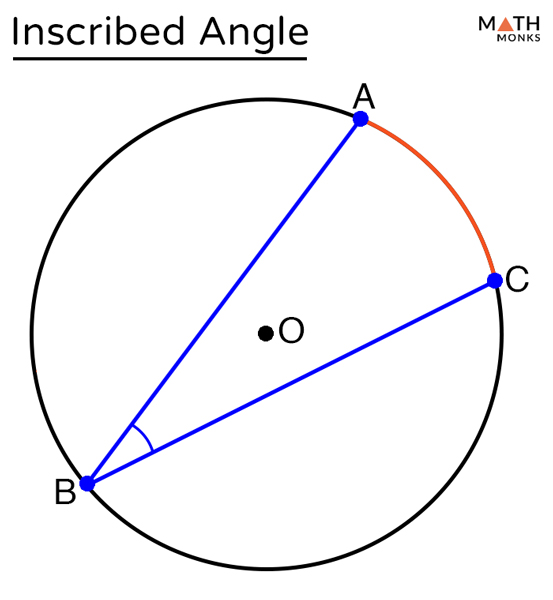
Inscribed Angle Definition Formula Theorem With Examples According to the inscribed angle theorem, the measure of the inscribed angle is half the measure of the central angle, ∠abc = 2∠cda. hence, ∠abc =2 x 20° = 40°. now, (4x 20)° = 40°. 4x = 40° 20°. x =20° 4 = 5°. what is an inscribed angle of a circle and how to find their measure– its definition in geometry with formula, proof. Here we have an inscribed angle intercepting an arc, so we can use the inscribed angle theorem. we can start out with mab = 2 × m∠acb, and then substitute 42° for m∠acb. that'll give us mab = 2 × 42°, or mab = 84°. sample problem. given that ∠acb is inscribed in circle ⊙o with radius 5 cm containing points a and b, and that m∠acb. By inscribed angle theorem, the size of the central angle = 2 x the size of the inscribed angle. given, 60° = inscribed angle. substitute. the size of the central angle = 2 x 60°. = 120°. example 2. given that ∠ qrp = (2x 20) ° and ∠ psq = 30°, find the value of x. Example 1: central angle theorem. find the measure of angle a a in circle d. d. recall the theorem. angle a a is an inscribed angle and is half the measure of the arc it intercepts. 2 solve the problem. arc pc pc is the intercepted arc of angle a. a. arc pc=42^ {\circ} pc = 42∘ and angle a a is an inscribed angle.
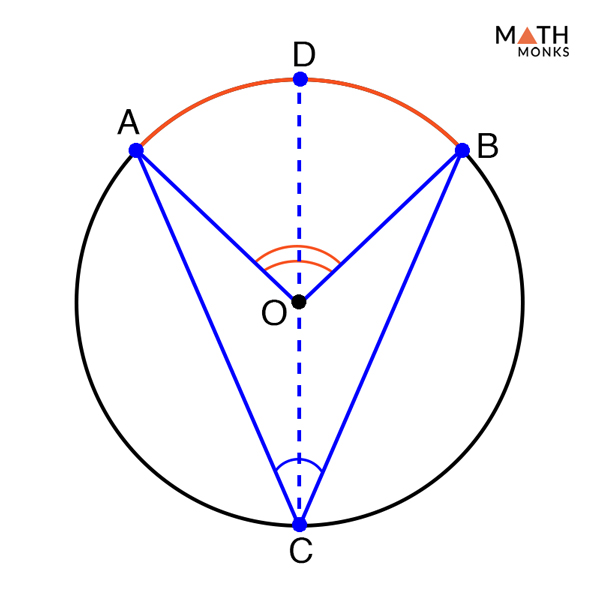
Inscribed Angle Definition Formula Theorem With Examples By inscribed angle theorem, the size of the central angle = 2 x the size of the inscribed angle. given, 60° = inscribed angle. substitute. the size of the central angle = 2 x 60°. = 120°. example 2. given that ∠ qrp = (2x 20) ° and ∠ psq = 30°, find the value of x. Example 1: central angle theorem. find the measure of angle a a in circle d. d. recall the theorem. angle a a is an inscribed angle and is half the measure of the arc it intercepts. 2 solve the problem. arc pc pc is the intercepted arc of angle a. a. arc pc=42^ {\circ} pc = 42∘ and angle a a is an inscribed angle. The angle at the centre of a circle is twice any angle at the circumference subtended by the same arc. the following diagrams illustrates the inscribed angle theorem. example: the center of the following circle is o. bod is a diameter of the circle. find the value of x. solution: ∠boc 70˚ = 180˚. Strategy. when proving the inscribed angle theorem, we will need to consider 3 separate cases: the first is when one of the chords is the diameter. the second case is where the diameter is in the middle of the inscribed angle. and the third case is when the diameter is outside the inscribed angle. these three cases cover all the possibilities.
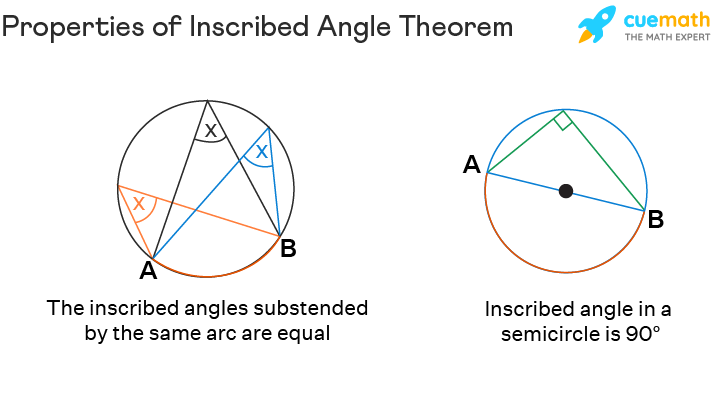
Inscribed Angle Theorem Definition Theorem Proof Examples The angle at the centre of a circle is twice any angle at the circumference subtended by the same arc. the following diagrams illustrates the inscribed angle theorem. example: the center of the following circle is o. bod is a diameter of the circle. find the value of x. solution: ∠boc 70˚ = 180˚. Strategy. when proving the inscribed angle theorem, we will need to consider 3 separate cases: the first is when one of the chords is the diameter. the second case is where the diameter is in the middle of the inscribed angle. and the third case is when the diameter is outside the inscribed angle. these three cases cover all the possibilities.
Inscribed Angle Definition Formula Theorem With Examples

Inscribed Angle Theorem Definition Theorem Proof Examples

Comments are closed.