Inscribed Angle Everything You Need To Know 2019
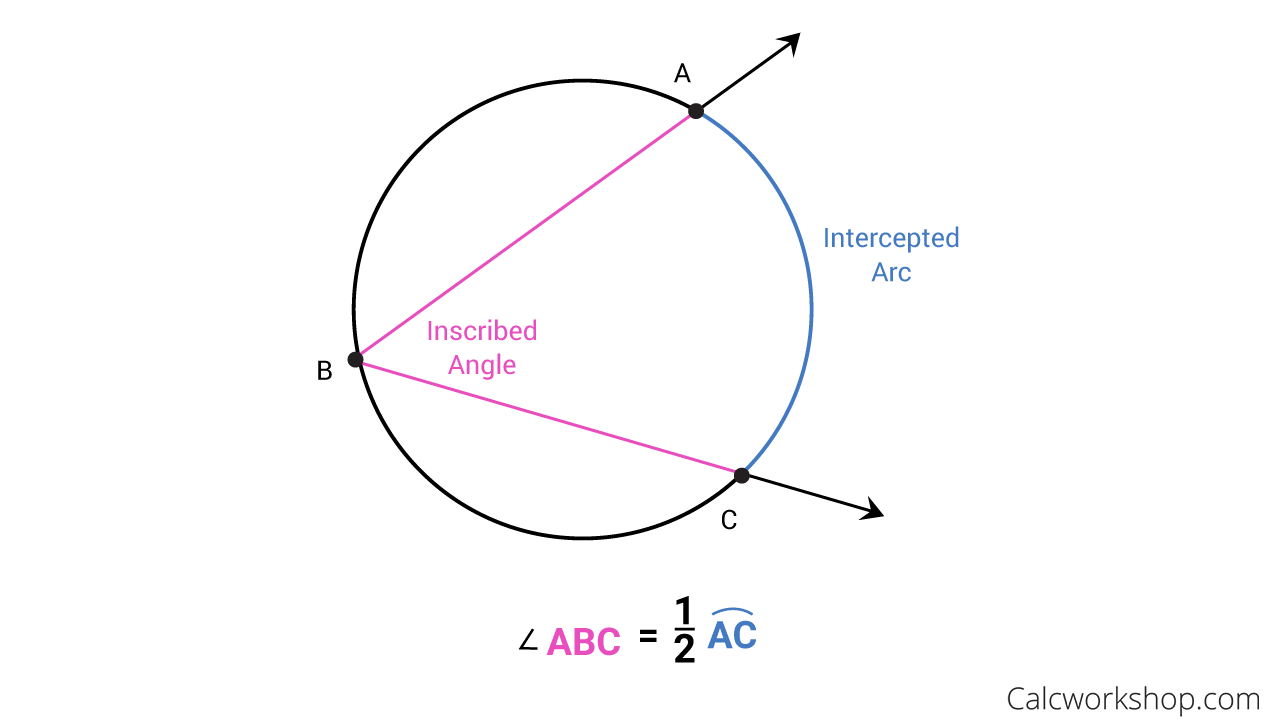
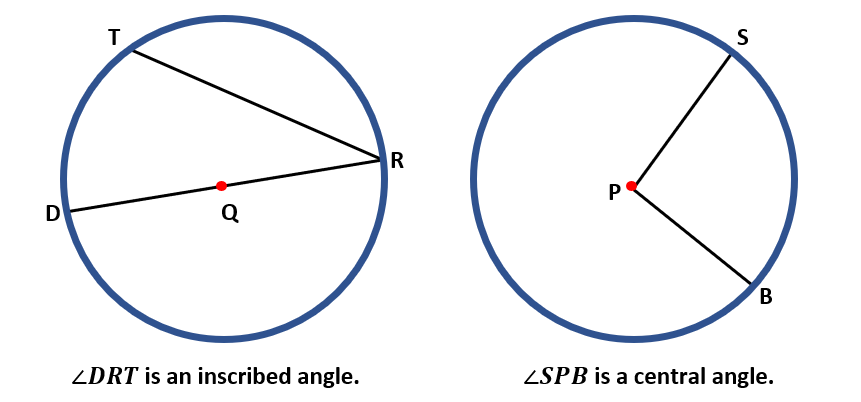
Inscribed Angle Everything You Need To Know 2019 An inscribed angle is an angle whose vertex is on a circle and whose sides contain chords of a circle. this is different than the central angle, whose vertex is at the center of a circle. if you recall, the measure of the central angle is congruent to the measure of the minor arc. however, when dealing with inscribed angles, the inscribed angle. Head to our arc length calculator! if you're burning with the question how to calculate the arc length with an inscribed angle, we shall combine the above relation with the inscribed angle formula to obtain the following: l = 2 \cdot \theta i \cdot r l = 2 ⋅ θi ⋅ r. ⚠️ make sure the angles are in radians before using the arc length.

Inscribed Angle Everything You Need To Know 2019 59 Off According to the inscribed angle theorem, the measure of the inscribed angle is half the measure of the central angle, ∠abc = 2∠cda. hence, ∠abc =2 x 20° = 40°. now, (4x 20)° = 40°. 4x = 40° 20°. x =20° 4 = 5°. what is an inscribed angle of a circle and how to find their measure– its definition in geometry with formula, proof. Example 2: find the missing angle x in the diagram below. solution: we need to find the value of x. one angle is given as 80°. by inscribed angle theorem we know that the central angle = 2 × inscribed angle. x = 2 × 80. x = 160. therefore, the value of x = 160°. become a problem solving champ using logic, not rules. Supplementary inscribed angle θ on minor arc. in geometry, an inscribed angle is the angle formed in the interior of a circle when two chords intersect on the circle. it can also be defined as the angle subtended at a point on the circle by two given points on the circle. equivalently, an inscribed angle is defined by two chords of the circle. Strategy. when proving the inscribed angle theorem, we will need to consider 3 separate cases: the first is when one of the chords is the diameter. the second case is where the diameter is in the middle of the inscribed angle. and the third case is when the diameter is outside the inscribed angle. these three cases cover all the possibilities.
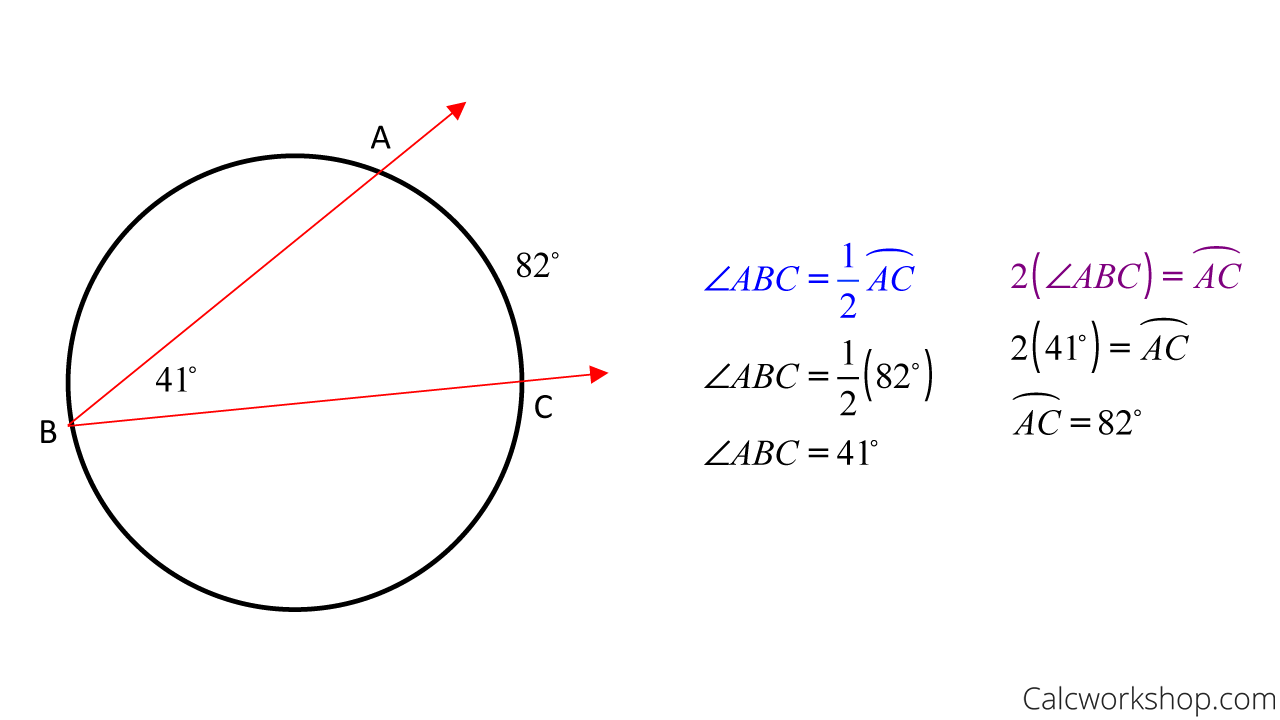
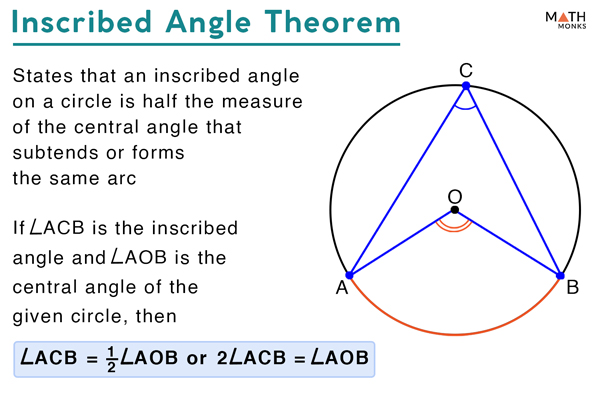
Inscribed Angle Everything You Need To Know 2019 Supplementary inscribed angle θ on minor arc. in geometry, an inscribed angle is the angle formed in the interior of a circle when two chords intersect on the circle. it can also be defined as the angle subtended at a point on the circle by two given points on the circle. equivalently, an inscribed angle is defined by two chords of the circle. Strategy. when proving the inscribed angle theorem, we will need to consider 3 separate cases: the first is when one of the chords is the diameter. the second case is where the diameter is in the middle of the inscribed angle. and the third case is when the diameter is outside the inscribed angle. these three cases cover all the possibilities. From the measure of an inscribed angle theorem, you know that m rs = 2m∠rus = 2(31°) = 62°. also, m∠str = —1 2 m rs = 1— 2 (62°) = 31°. so, ∠str ≅∠rus. example 2 suggests the inscribed angles of a circle theorem. theorem theorem 10.11 inscribed angles of a circle theorem if two inscribed angles of a circle intercept. The total measure of the opposite angles of a quadrilateral inscribed in a circle is 180°. it means that they are supplementary angles. let us say, for example, in the figure below, the points q, u, a, and d form an inscribed quadrilateral. ∠q, ∠u, ∠a, and ∠d are all inscribed angles. ∠q and ∠a are supplementary.
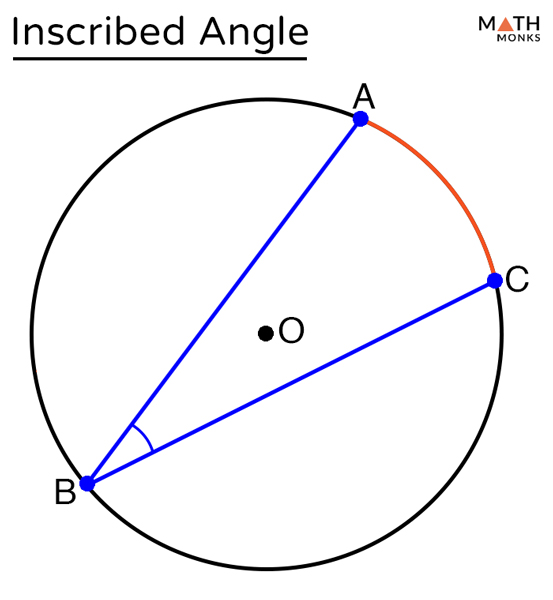
Inscribed Angle Examples From the measure of an inscribed angle theorem, you know that m rs = 2m∠rus = 2(31°) = 62°. also, m∠str = —1 2 m rs = 1— 2 (62°) = 31°. so, ∠str ≅∠rus. example 2 suggests the inscribed angles of a circle theorem. theorem theorem 10.11 inscribed angles of a circle theorem if two inscribed angles of a circle intercept. The total measure of the opposite angles of a quadrilateral inscribed in a circle is 180°. it means that they are supplementary angles. let us say, for example, in the figure below, the points q, u, a, and d form an inscribed quadrilateral. ∠q, ∠u, ∠a, and ∠d are all inscribed angles. ∠q and ∠a are supplementary.
Inscribed Angles Problems And Answers
Inscribed Angle Examples

Comments are closed.