In The Given Figure Two Circles With Centres A And B Of Radii 5 Cm And

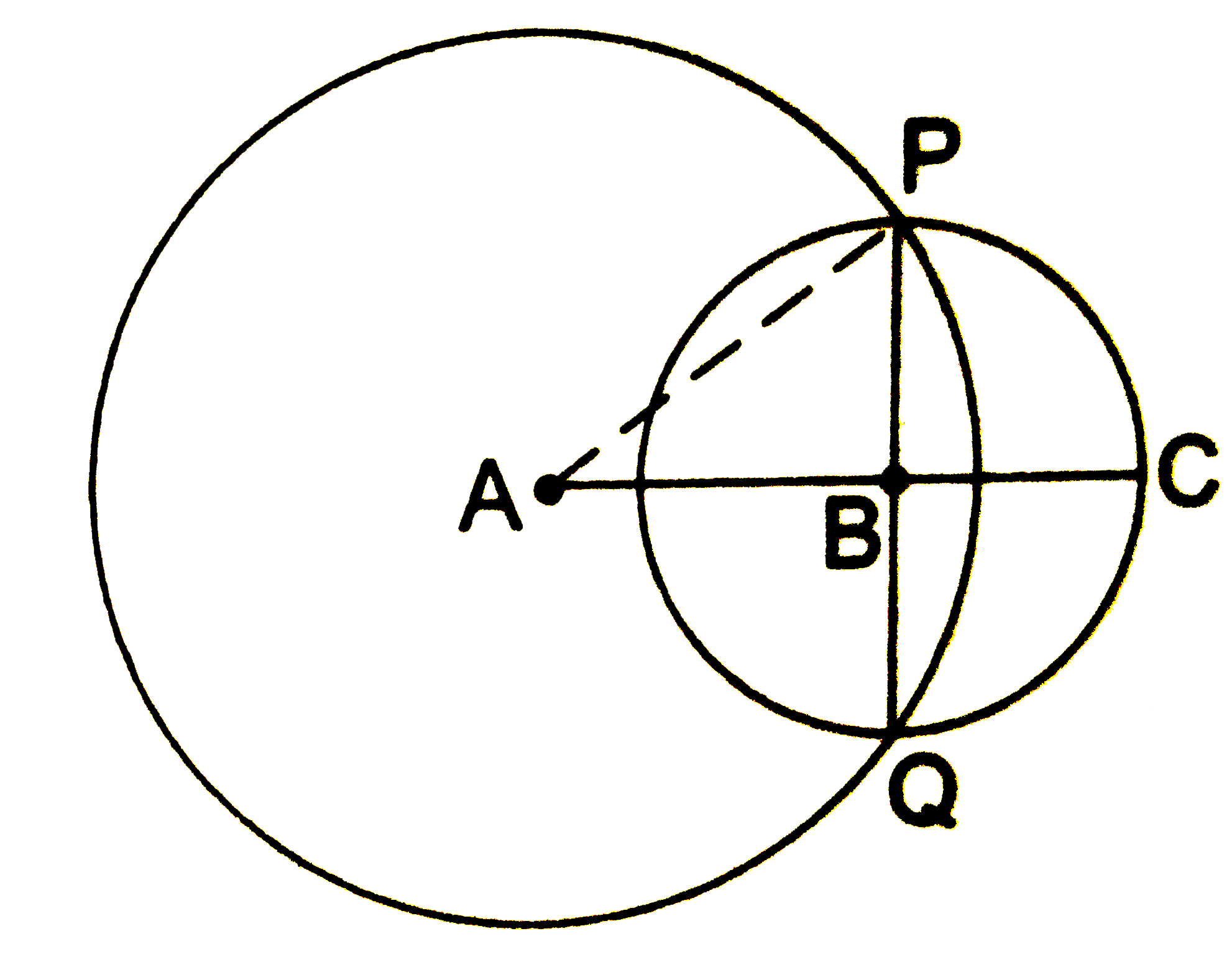
In The Given Figure A And B Are The Centres Of Two Circles Having Ra The given figure shows two circles with centres a and b; and radii 5 cm and 3 cm respectively, touching each other internally. if the perpendicular bisector of ab meets the bigger circle in p and q, find the length of pq. The given figure shows two circles with centres a and b; and radii 5 cm and 3 cm respectively, touching each other internally. if the perpendicular bisector of ab meets the bigger circle in p and q, find the length of pq.

In The Given Figure Two Circles With Centres A And B Of Radii 5 Cm And Two circles with centres a and b and of radii 5 cm and 3 cm touch each other internally. length of pq. if two circles touch internally then distance between their centers is equal to the difference of their radii. so, ab = (5 3) cm. ab= 2 cm. also , the common chord pq is the perpendicular bisector of ab. ∴ ac = cb = 1 cm. Given oa = ob = 15 cm and op = 9 cm. calculate the length of: (i) cd (ii) ad (iii) cb . in the given figure, ac is a diameter of circle, centre o. chord bd is perpendicular to ac. write down the angles p, q and r in terms of x. in the given figure, o is the centre of the circle with radius 5 cm. op and oq are perpendicular to ab and cd. A and b are the centres of the circles with radii 5cm and 3cm respectively. c is the mid point of ab. extend ab upto o point on circumference of outer circle. ab = ao− bo = 5 −3 = 2cm (since ao and bo are radii of larger and smaller circles) ac = ab 2 = 2 2 = 1cm. now in right angled triangle amp,ac = 1cm,ap = 5cm. Bq = 5 cm (length from q to b) ps = 12 cm (tangent from p to the smaller circle) qt = 3 cm (tangent from q to the larger circle) according to the tangent property: we know that as and bt are the radii of the circles. since the circles touch externally at k, the radii add up to the length of segment pq: now, we can set up equations using the.

In The Given Figure A And B Are The Centres Of Two Circles Having A and b are the centres of the circles with radii 5cm and 3cm respectively. c is the mid point of ab. extend ab upto o point on circumference of outer circle. ab = ao− bo = 5 −3 = 2cm (since ao and bo are radii of larger and smaller circles) ac = ab 2 = 2 2 = 1cm. now in right angled triangle amp,ac = 1cm,ap = 5cm. Bq = 5 cm (length from q to b) ps = 12 cm (tangent from p to the smaller circle) qt = 3 cm (tangent from q to the larger circle) according to the tangent property: we know that as and bt are the radii of the circles. since the circles touch externally at k, the radii add up to the length of segment pq: now, we can set up equations using the. The given figure show two circles with centres a and b; and radii 5 cm and 3cm respectively, touching each other internally. if the perpendicular bisector of ab meets the bigger circle in p and q, find the length of pq. solution: question 4. in the given figure, chord ed is parallel to diameter ac of the circle. given ∠ cbe = 65°, calculate. Detailed solution. download solution pdf. two circles with centres a and b of radii 5 cm and 3 cm respectively touch each other internally. ∴ ab = 5 – 3 = 2 cm. the perpendicular bisector of ab meets the bigger circle in p and q. let perpendicular bisector bisects ab at c. ∴ ac = ab 2 = 1 cm. Δ acb is right angled triangle at c.

In The Given Figure Two Circles With Centres A And B Of Radii 5 Cm And The given figure show two circles with centres a and b; and radii 5 cm and 3cm respectively, touching each other internally. if the perpendicular bisector of ab meets the bigger circle in p and q, find the length of pq. solution: question 4. in the given figure, chord ed is parallel to diameter ac of the circle. given ∠ cbe = 65°, calculate. Detailed solution. download solution pdf. two circles with centres a and b of radii 5 cm and 3 cm respectively touch each other internally. ∴ ab = 5 – 3 = 2 cm. the perpendicular bisector of ab meets the bigger circle in p and q. let perpendicular bisector bisects ab at c. ∴ ac = ab 2 = 1 cm. Δ acb is right angled triangle at c.

In The Figure Two Circles With Centres A And B And Of Radii 5cm And