In Exercises 7 14 Find The General Solution Of The First Order Linear Differential Equation For X

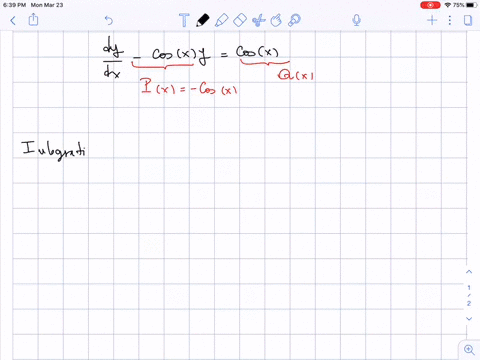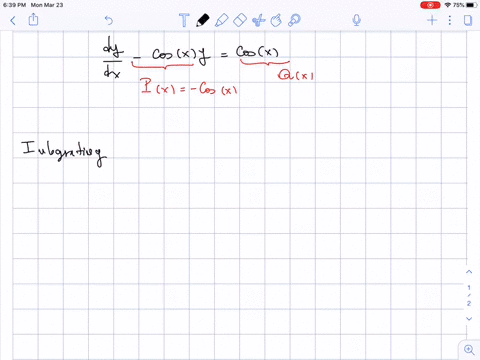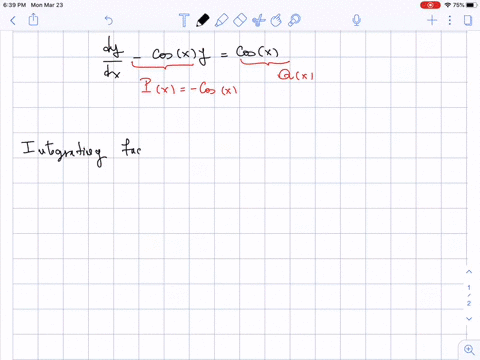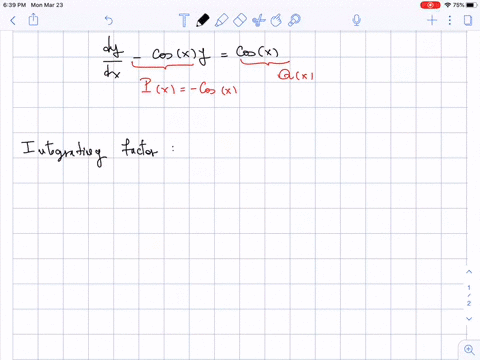
Solved In Exercises 7 14 Find The General Solution Of The First Order Question: find the general solution of the first order linear differential equation y' (ln x)y = 3 x^x. y (x)= note: use c for the arbitrary constant. find the general solution of the first order linear differential equation y' (ln x)y = 3 x^x. y (x)=. note: use c for the arbitrary constant. there are 2 steps to solve this one. 4) you can determine the behavior of all first order differential equations using directional fields or euler’s method. solution: \(\displaystyle t\) for the following problems, find the general solution to the differential equations. 5) \(\displaystyle y′=x^2 3e^x−2x\) 6) \(\displaystyle y'=2^x cos^{−1}x\).

Solved In Exercises 7 14 Find The General Solution Of The First Order First order linear diferential equations. put into the formdy1 psxdy − qsxd dxwhere p and q are. continuous functions on a given interval. this type of equation occurs frequ. be written in the form21y9 1 y − 2xnotice that this differential equation is not separable because it’s impossible to factor the expression for y9. First order linear differential equation: the first order differential equation y0 = f(x,y)isalinear equation if it can be written in the form y0 p(x)y = q(x) (1) where p and q are continuous functions on some interval i. differential equations that are not linear are called nonlinear equations. solution method: step 1. This gives the general solution to (2) x(t) = ce− p(t)dt where c = any value. (3) a useful notation is to choose one specific solution to equation (2) and call it x h(t). then the solution (3) shows the general solution to the equation is x(t) = cx h(t). (4) there is a subtle point here: formula (4) requires us to choose one solution to name x. 3.1. homogeneous and inhomogeneous; superposition. a first order linear equation is homogeneous if the right hand side is zero: (1) x ̇ p(t)x = 0 . homogeneous linear equations are separable, and so the solution can be expressed in terms of an integral. the general solution is. (2) − x = ±. r p(t)dt e or x = 0 .

Solved In Exercises 7 14 Find The General Solution Of The First Order This gives the general solution to (2) x(t) = ce− p(t)dt where c = any value. (3) a useful notation is to choose one specific solution to equation (2) and call it x h(t). then the solution (3) shows the general solution to the equation is x(t) = cx h(t). (4) there is a subtle point here: formula (4) requires us to choose one solution to name x. 3.1. homogeneous and inhomogeneous; superposition. a first order linear equation is homogeneous if the right hand side is zero: (1) x ̇ p(t)x = 0 . homogeneous linear equations are separable, and so the solution can be expressed in terms of an integral. the general solution is. (2) − x = ±. r p(t)dt e or x = 0 . Let g = g(t) be the number of units in the patient’s bloodstream at time t> 0. then g ′ = − λg r, where the first term on the right is due to the absorption of the glucose by the patient’s body and the second term is due to the injection. determine g for t> 0, given that g(0) = g0. also, find limt → ∞g(t). The next simplest equation is the riccati equation y = a(x) b(x)y c(x)y 2 , where the right hand side is now a quadratic function of y instead of a linear function. in general the riccati equation is not solvable by elementary means. however, a) show that if y1(x) is a solution, then the general solution is y = y1 u,.