If A Transversal Intersects Two Lines Such That The Bisectors Of A Pair Of Corresponding Angles Are

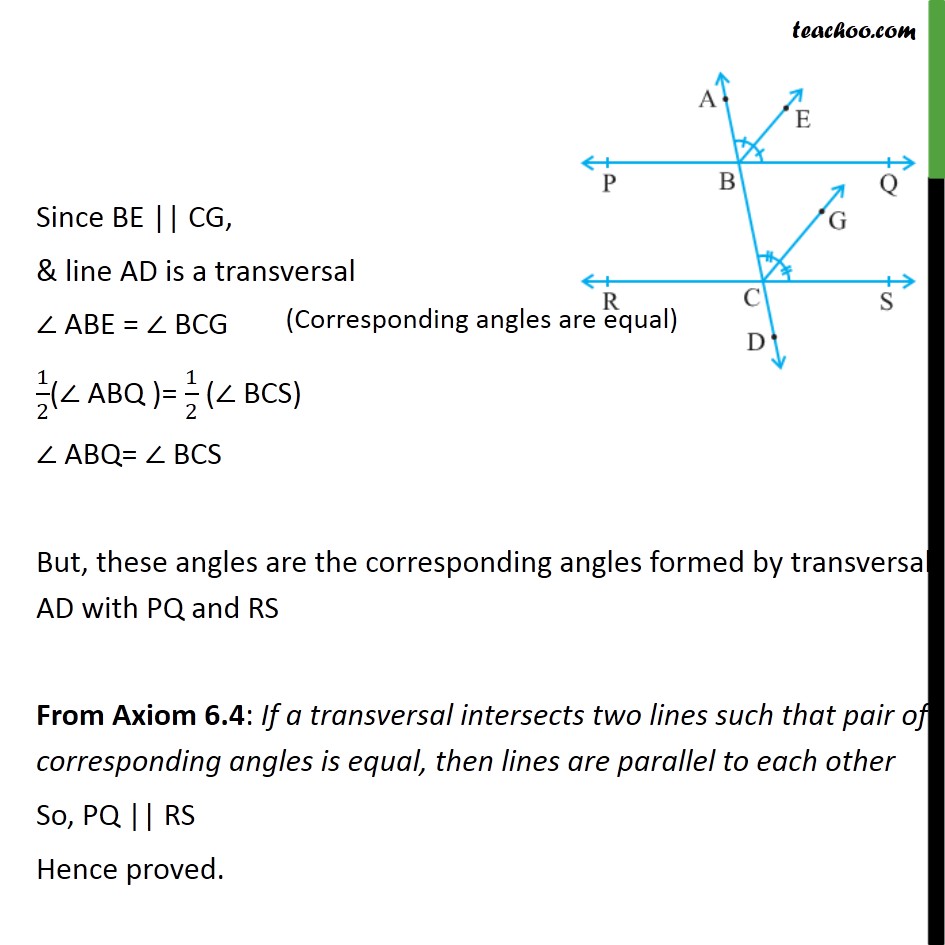
Example 5 If A Transversal Intersects Two Lines Such That Examples Transcript. example 5 if a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel. in figure, transversal ad intersects two lines pq and rs at points b and c respectively. ray be is the bisector of bacq so , abe = ebq = 1 2 ( abq ) and ray cg is the. If a transversal intersects two parallel lines then show that the bisectors of any pair of alternate angles are also parallel. q. if the bisector of the pair alternate interior angle framed by a transversal with two given lines are parallel.

If A Transversal Intersects Two Lines Such That The Bisectors Of A Pair If a traversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel , then p.t. the two lines are parallel. view solution q 4. Now use the converse of the corresponding angle theorem to prove two lines parallel. complete step by step answer: here we have to prove that if a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel. let us represent this situation diagrammatically. 1. identify the given information: we have two lines, pq and rs, intersected by a transversal ad. the bisectors of a pair of corresponding angles, be and cg, are given to be parallel. 2. label the angles: let angle abq be one of the corresponding angles formed by the transversal ad and line pq. let angle bcg be the corresponding angle formed by. Example 3 : in fig. 6.11, op, oq, or and os are four rays. prove that ∠ poq ∠ qor ∠ sor ∠ pos = 360°.#linesandanglesclass9.

If A Transversal Intersects Two Lines Such That The Bisectors Of A Pair 1. identify the given information: we have two lines, pq and rs, intersected by a transversal ad. the bisectors of a pair of corresponding angles, be and cg, are given to be parallel. 2. label the angles: let angle abq be one of the corresponding angles formed by the transversal ad and line pq. let angle bcg be the corresponding angle formed by. Example 3 : in fig. 6.11, op, oq, or and os are four rays. prove that ∠ poq ∠ qor ∠ sor ∠ pos = 360°.#linesandanglesclass9. Click here👆to get an answer to your question ️ if a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel. A transversal intersects two parallel lines. prove that the bisectors of any pair of corresponding angles so formed are parallel. summary: an angle bisector or the bisector of an angle is a ray that divides an angle into two equal parts. a transversal intersects two parallel lines. it is proven that the bisectors of any pair of corresponding.

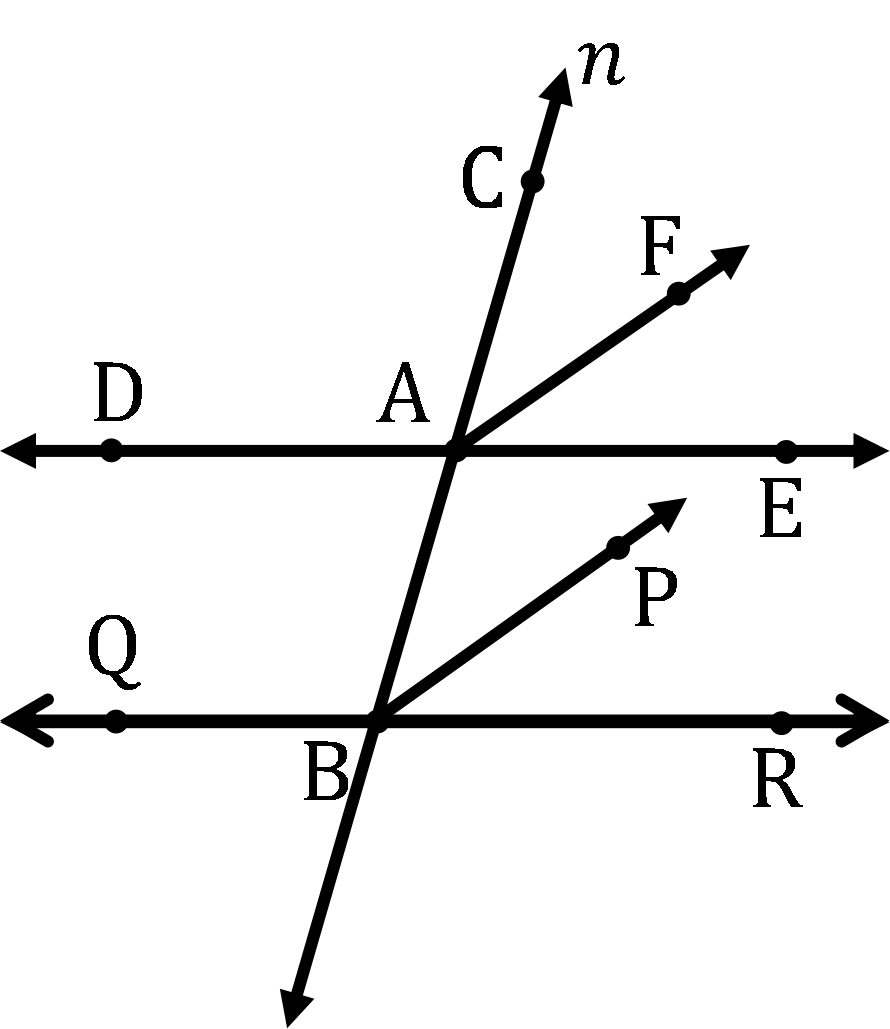
A Transversal Intersects Two Parallel Lines Prove That The Bisectors Of Click here👆to get an answer to your question ️ if a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel. A transversal intersects two parallel lines. prove that the bisectors of any pair of corresponding angles so formed are parallel. summary: an angle bisector or the bisector of an angle is a ray that divides an angle into two equal parts. a transversal intersects two parallel lines. it is proven that the bisectors of any pair of corresponding.