If A Transversal Intersects Two Lines Such A Pair Of Corresponding Angles Is Equal Then The Two

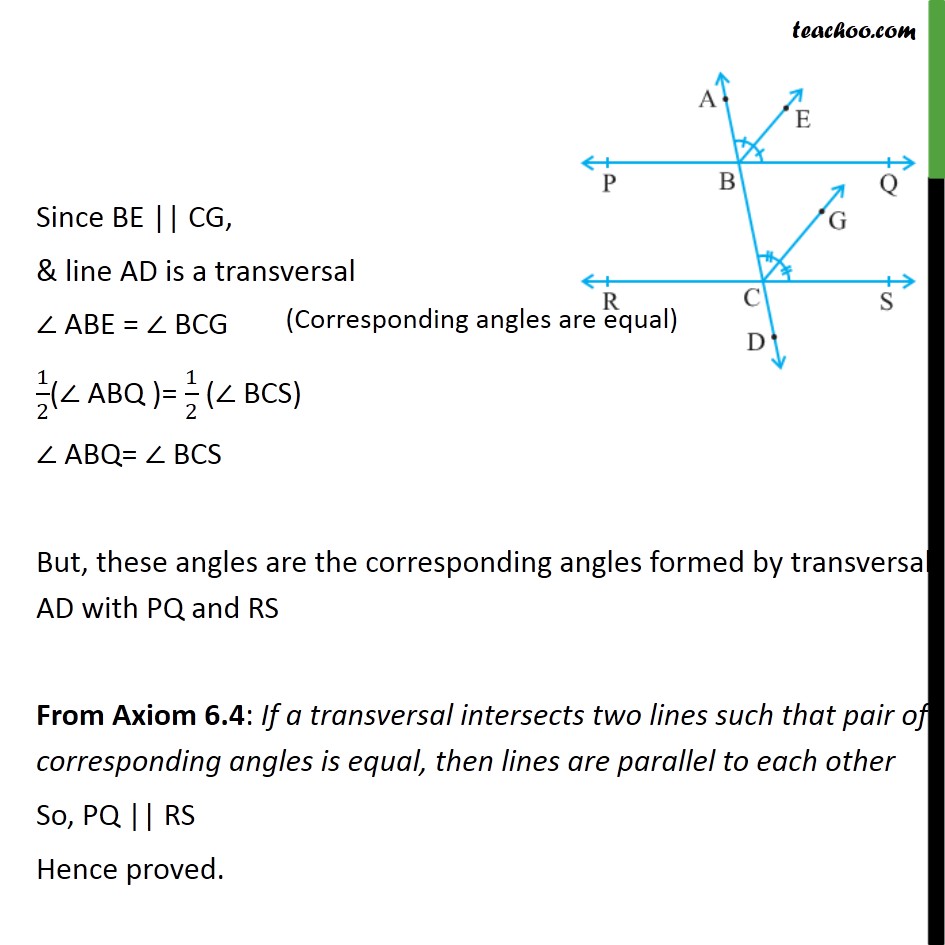
Example 5 If A Transversal Intersects Two Lines Such That Examples Transcript. example 5 if a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel. in figure, transversal ad intersects two lines pq and rs at points b and c respectively. ray be is the bisector of bacq so , abe = ebq = 1 2 ( abq ) and ray cg is the. A transversal is defined as a line that passes through two lines in the same plane at two distinct points in the geometry. a transversal intersection with two lines produces various types of angles in pairs, such as consecutive interior angles, corresponding angles and alternate angles. a transversal produces 8 angles and this can be observed.

Example 5 If A Transversal Intersects Two Lines Such That If a traversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel , then p.t. the two lines are parallel. view solution q 4. According to the corresponding angles postulate if a transversal intersects two parallel lines, the corresponding angles will be always equal. s o, ∠ e p b = ∠ p q d ½ ∠ e p b = ½ ∠ p q d ∠ e p r = ∠ p q s. but, we also know that they are corresponding angles of p r and q s. since the corresponding angles are equal, we have, p r. If a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel ans: hint: first of all draw the diagram of information given in the question to visualize the. What if a transversal intersects two lines and the pair of corresponding angles are equal? then, the two lines intersected by the transversal are said to be parallel. this is the converse of the corresponding angle theorem. important notes on corresponding angles: when two parallel lines are intersected by a third one, the angles that occupy.

If A Transversal Intersects Two Lines Such A Pair Of Corresponding If a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel ans: hint: first of all draw the diagram of information given in the question to visualize the. What if a transversal intersects two lines and the pair of corresponding angles are equal? then, the two lines intersected by the transversal are said to be parallel. this is the converse of the corresponding angle theorem. important notes on corresponding angles: when two parallel lines are intersected by a third one, the angles that occupy. Given, a transversal intersects two parallel lines. we have to prove that the bisectors of any pair of corresponding angles formed are parallel. consider two parallel lines ab and cd cut by a transversal hg. we know that if a transversal intersects two parallel lines, then corresponding angles are equal and conversely. the corresponding angles. When a transversal is formed by intersecting two parallel lines, then the following properties can be defined. 1. if a transversal cuts two parallel lines, each pair of corresponding angles are equal in measure. 2. if a transversal cuts two parallel lines, each pair of alternate interior angles are equal. 3.