If A Transversal Intersects A Pair Of Lines In Such A Way That A Pair

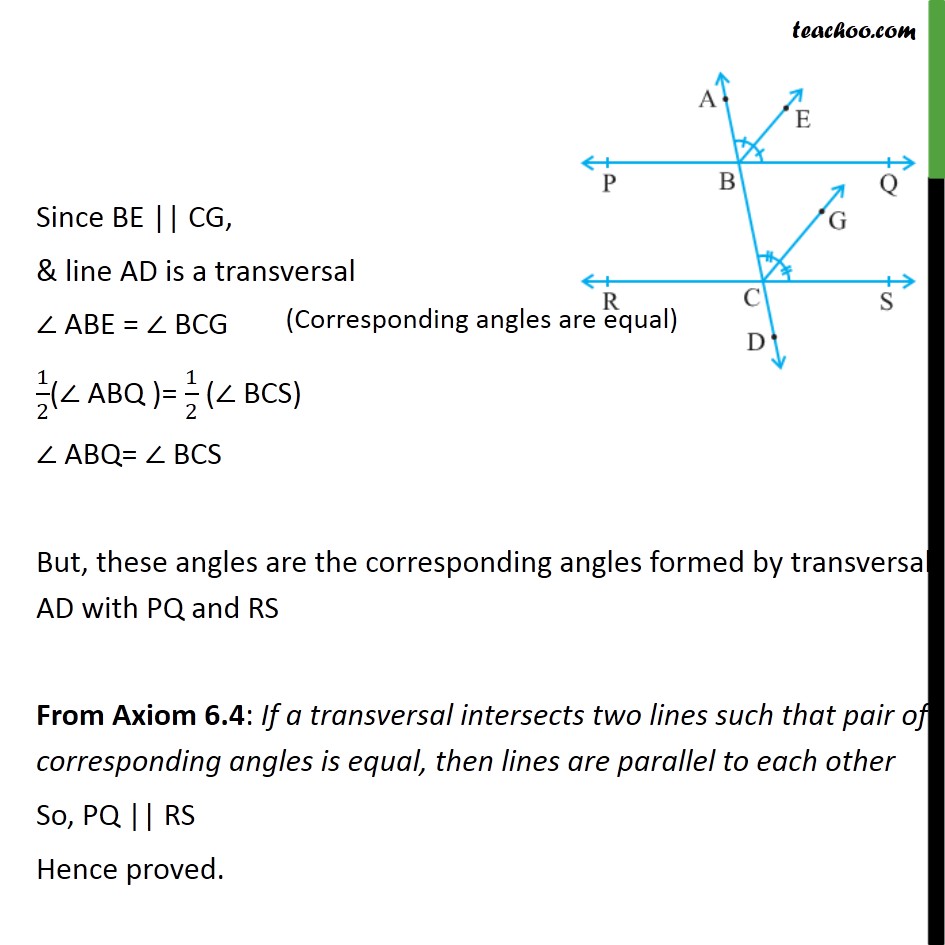
If A Transversal Intersects A Pair Of Lines In Such A Way That A Pair Transcript. example 5 if a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel. in figure, transversal ad intersects two lines pq and rs at points b and c respectively. ray be is the bisector of bacq so , abe = ebq = 1 2 ( abq ) and ray cg is the. Various theorems are defined for transversal, such as: 1. if a transversal intersects two parallel lines, then each pair of corresponding angles is equal. 2. if a transversal intersects two lines such that a pair of corresponding angles are equal, then the two lines are parallel to each other. 3.

If A Transversal Intersects A Pair Of Lines In Such A Way That A Pair If a traversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel , then p.t. the two lines are parallel. view solution q 4. Now use the converse of the corresponding angle theorem to prove two lines parallel. complete step by step answer: here we have to prove that if a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel. let us represent this situation diagrammatically. Thus, the sum of the interior angles on the same side of the line p and between the lines l and m is 180 ∘. therefore, l and m are parallel. hence, if a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then the two lines are parallel. Transversal lines. in geometry, a transversal is a line that passes through two lines in the same plane at two distinct points. transversals play a role in establishing whether two or more other lines in the euclidean plane are parallel. the intersections of a transversal with two lines create various types of pairs of angles: consecutive.

If A Transversal Intersects Two Lines In Such A Way That A Pair Of Thus, the sum of the interior angles on the same side of the line p and between the lines l and m is 180 ∘. therefore, l and m are parallel. hence, if a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then the two lines are parallel. Transversal lines. in geometry, a transversal is a line that passes through two lines in the same plane at two distinct points. transversals play a role in establishing whether two or more other lines in the euclidean plane are parallel. the intersections of a transversal with two lines create various types of pairs of angles: consecutive. Conversely, if a transversal intersects two lines in such a way that a pair of consecutive interior angles are supplementary, then the two lines are parallel. parallel lines property. the parallel lines property is a transitive property that can be applied to parallel lines. it states that if lines l ∥ m and m ∥ n, then l ∥ n. Various theorems are defined for transversal, such as: 1. if a transversal intersects two parallel lines, then each pair of corresponding angles is equal. 2. if a transversal intersects two lines such that a pair of corresponding angles are equal, then the two lines are parallel to each other. 3.

Example 5 If A Transversal Intersects Two Lines Such That Examples Conversely, if a transversal intersects two lines in such a way that a pair of consecutive interior angles are supplementary, then the two lines are parallel. parallel lines property. the parallel lines property is a transitive property that can be applied to parallel lines. it states that if lines l ∥ m and m ∥ n, then l ∥ n. Various theorems are defined for transversal, such as: 1. if a transversal intersects two parallel lines, then each pair of corresponding angles is equal. 2. if a transversal intersects two lines such that a pair of corresponding angles are equal, then the two lines are parallel to each other. 3.