Ideal Gases Specific Heat Internal Energy Enthalpy Thermodynamics

Ideal Gases Specific Heat Internal Energy Enthalpy Thermodynamics Learn about how specific heat, internal energy and enthalpy work with ideal gases. we go through constant volume and constant pressure specific volume, how e. The simple relations between changes in energy (or enthalpy) and temperature are a consequence of the behavior of an ideal gas, specifically the dependence of the energy and enthalpy on temperature only, and are not true for more complex substances. 2. 4. 2. 4. 2 reversible adiabatic processes for an ideal gas from the first law, with , , and ,.

Example Using Specific Heat To Calculate Ideal Gas Internal Energy Average particle speed in a gas. we can use equation 5.5.2 and equation 5.5.14 to draw another conclusion about the particles in this gas: u = 3 2nkbt ⇒ u ≡ u n = 3 2kbt. this tells us that the average energy per particle u is a constant times the temperature of the gas. The monoatomic ideal gas constant volume specific heat c v ¯ is one of the more remarkable theoretical results the first four periodic gases in the periodic table all have molar specific heats of 12.5 j mol 1 k 1 under conditions of constant volume, and deviations for the larger ideal gases are minor and only in the third significant figure. At constant pressure, the change in the enthalpy of a system is equal to the heat flow: Δh = qp Δ h = q p. example 5.3.1 5.3. 1. the molar enthalpy of fusion for ice at 0.0°c and a pressure of 1.00 atm is 6.01 kj, and the molar volumes of ice and water at 0°c are 0.0197 l and 0.0180 l, respectively. Heat capacities at constant volume and pres sure. by combining the ̄rst law of thermodynamics with the de ̄nition of heat capac ity, we can develop general expressions for heat capacities at constant volume and constant pressure. writing the ̄rst law in the form q = e p v; and insering this into c = q 4 4 ; we arrive at 4t.
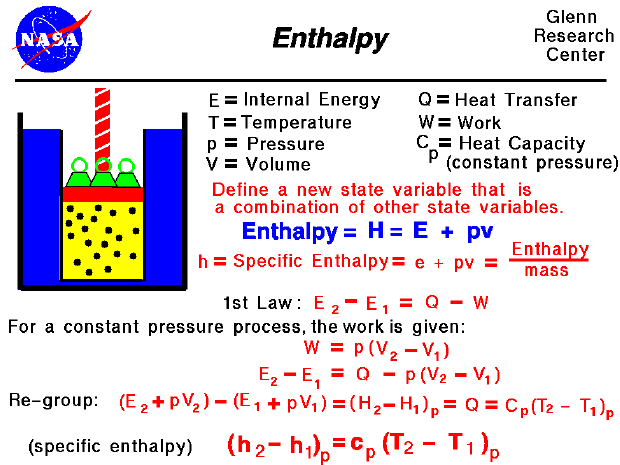
Enthalpy At constant pressure, the change in the enthalpy of a system is equal to the heat flow: Δh = qp Δ h = q p. example 5.3.1 5.3. 1. the molar enthalpy of fusion for ice at 0.0°c and a pressure of 1.00 atm is 6.01 kj, and the molar volumes of ice and water at 0°c are 0.0197 l and 0.0180 l, respectively. Heat capacities at constant volume and pres sure. by combining the ̄rst law of thermodynamics with the de ̄nition of heat capac ity, we can develop general expressions for heat capacities at constant volume and constant pressure. writing the ̄rst law in the form q = e p v; and insering this into c = q 4 4 ; we arrive at 4t. The internal energy of an ideal gas is therefore directly proportional to the temperature of the gas. e sys = 3 2 rt. in this equation, r is the ideal gas constant in joules per mole kelvin (j mol k) and t is the temperature in kelvin. the internal energy of systems that are more complex than an ideal gas can't be measured directly. In the preceding chapter, we found the molar heat capacity of an ideal gas under constant volume to be. cv = d 2r, (3.6.10) (3.6.10) c v = d 2 r, where d is the number of degrees of freedom of a molecule in the system. table 3.6.1 3.6. 1 shows the molar heat capacities of some dilute ideal gases at room temperature.

Enthalpy The internal energy of an ideal gas is therefore directly proportional to the temperature of the gas. e sys = 3 2 rt. in this equation, r is the ideal gas constant in joules per mole kelvin (j mol k) and t is the temperature in kelvin. the internal energy of systems that are more complex than an ideal gas can't be measured directly. In the preceding chapter, we found the molar heat capacity of an ideal gas under constant volume to be. cv = d 2r, (3.6.10) (3.6.10) c v = d 2 r, where d is the number of degrees of freedom of a molecule in the system. table 3.6.1 3.6. 1 shows the molar heat capacities of some dilute ideal gases at room temperature.

Change In Internal Energy Using Specific Heat In 3 Minutes Youtube

Ppt Chapter 3 The First Law Of Thermodynamics Closed System

Comments are closed.