How Would You Use The Parallax Formula To Determine The Distances To A

What Is The Parallax Formula And How Is It Used To Calculate The The parallax formula states that the distance to a star is equal to 1 divided by the parallax angle, p, where p is measured in arc seconds, and d is parsecs. d=1 p parallax is a method of using two points of observation to measure the distance to an object by observing how it appears to move against a background. one way to understand parallax is to look at a nearby object and note its. The parallax formula for calculating approximate distance is: \quad d = \frac {1} {p} d = p 1. where: d. d d – distance between the star and the earth, measured in parsecs; and. p. p p – parallax angle, measured in arcseconds. using the above parallax equation, we can also define 1 parsec as the distance at which an object has a parallax of.
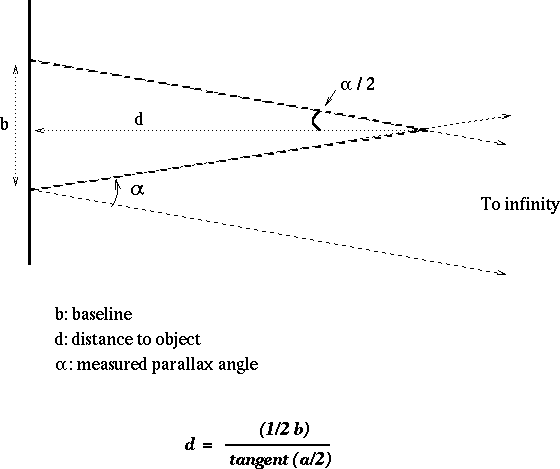
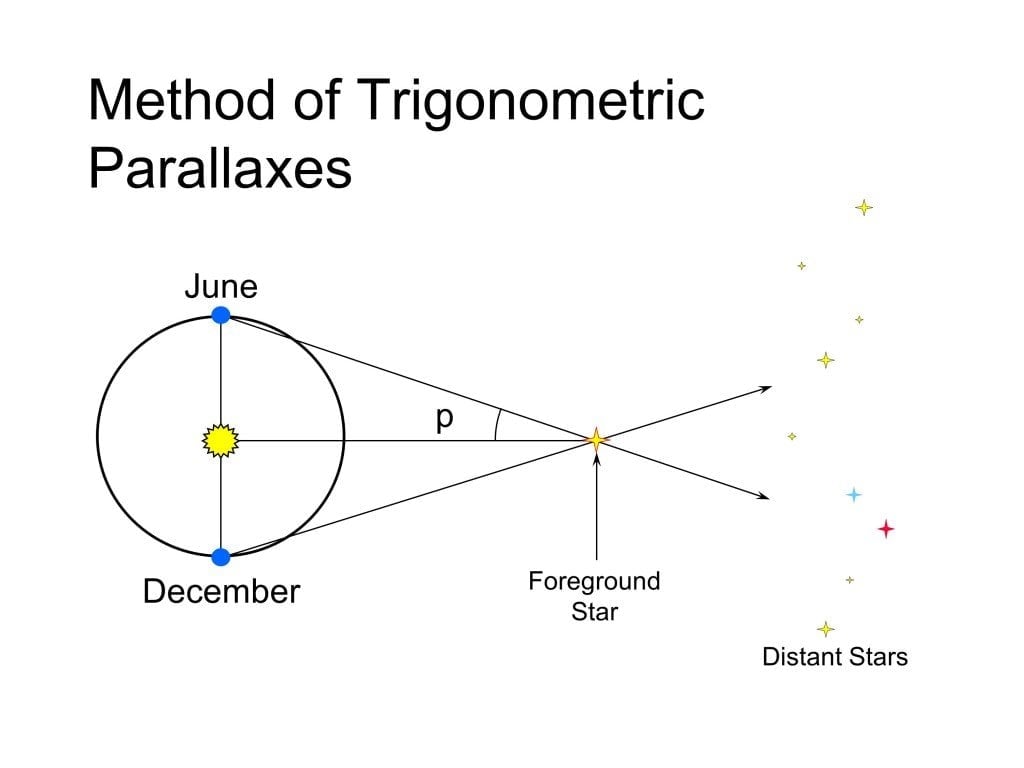
Parallax The parallax method, however, is only the first rung on the cosmic distance ladder, a succession of methods that astronomers use to estimate distances of objects in the universe. The parallax angle is 0.002790. how would you use the parallax formula to determine the distances to a star (in parsecs)? the parallax angle is 0.001293. the star wolf 1061 has a parallax of 2.34 arcseconds, while the star ross 652 has a parallax of 1.70 arc seconds. Exercise 17.2.1: use trigonometric parallax to estimate the distance to star cluster knox0325 in units of the earth sun distance, known as an astronomical unit or au. there are 60 arc seconds in an arc minute and 60 arc minutes in one degree. answer. the observed shift is actually 2p, with p as indicated in the diagram. A little basic trigonometry, here is how you nd the distance to an object using parallax: if you split your triangle in half (dotted line), then the tangent of ( =2) is equal to the quantity (b=2)=d: tan 2 = (b=2) d rearranging the equation gives: d= (b=2) tan( =2) you can determine the tangent of an angle using your calculator by entering the.
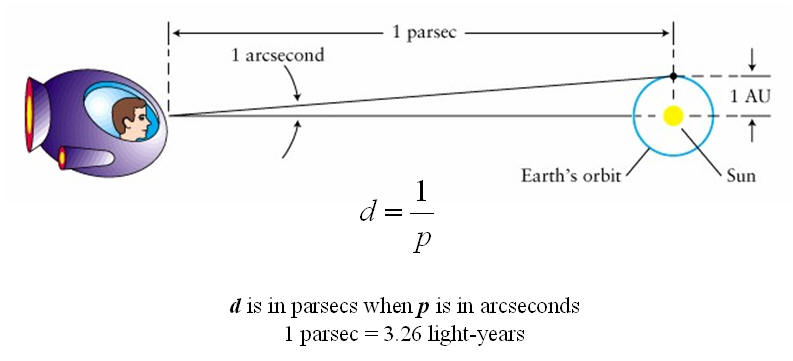
How Would You Use The Parallax Formula To Determine The Distances To A Exercise 17.2.1: use trigonometric parallax to estimate the distance to star cluster knox0325 in units of the earth sun distance, known as an astronomical unit or au. there are 60 arc seconds in an arc minute and 60 arc minutes in one degree. answer. the observed shift is actually 2p, with p as indicated in the diagram. A little basic trigonometry, here is how you nd the distance to an object using parallax: if you split your triangle in half (dotted line), then the tangent of ( =2) is equal to the quantity (b=2)=d: tan 2 = (b=2) d rearranging the equation gives: d= (b=2) tan( =2) you can determine the tangent of an angle using your calculator by entering the. We saw before that the smaller the parallax, the larger the distance. we can express this as a simple formula: where: p = parallax angle in arcseconds. d = distance in "parsecs". writing our parallax formula in this way allows us to define a new "natural" unit for distances in astronomy: the parallax second or parsec. Distances to astronomical objects can be one of the most difficult and important quantities to measure. one cannot simply stretch a tape measure out to the star vega for example (or even to the moon!). the first and most fundamental way to measure distances to the nearby stars is by making use of the well known phenomenon of parallax. parallax.
How Do You Measure The Distance To A Star Scienceabc We saw before that the smaller the parallax, the larger the distance. we can express this as a simple formula: where: p = parallax angle in arcseconds. d = distance in "parsecs". writing our parallax formula in this way allows us to define a new "natural" unit for distances in astronomy: the parallax second or parsec. Distances to astronomical objects can be one of the most difficult and important quantities to measure. one cannot simply stretch a tape measure out to the star vega for example (or even to the moon!). the first and most fundamental way to measure distances to the nearby stars is by making use of the well known phenomenon of parallax. parallax.

Determining Distances Using Parallax

How To Calculate Parallax

Comments are closed.