How To Find The Sum Of Interior Angles Of A Polygon

Sum Of Interior Angles In A Polygon Youtube If it is a regular polygon (all sides are equal, all angles are equal) shape sides sum of interior angles shape each angle; triangle: 3: 180° 60° quadrilateral: 4: 360° 90° pentagon: 5: 540° 108° hexagon: 6: 720° 120° heptagon (or septagon) 7: 900° 128.57 ° octagon: 8: 1080° 135° nonagon: 9: 1260° 140° any polygon: n (n−2. Categories: geometry. to calculate the sum of interior angles, start by counting the number of sides in your polygon. next, plug this number into the formula for the "n" value. then, solve for "n" by subtracting 2 from the number of sides and multiplying the difference by 180.

Sum Of Interior Angles Of A Polygon Worksheet With Answers Courses on khan academy are always 100% free. start practicing—and saving your progress—now: khanacademy.org math geometry home geometry shapes. To find the interior angle sum of a polygon, we can use a formula: interior angle sum = (n 2) x 180°, where n is the number of sides. for example, a pentagon has 5 sides, so its interior angle sum is (5 2) x 180° = 3 x 180° = 540°. The sum of all interior angles of a regular polygon is calculated by the formula s= (n 2) × 180°, where 'n' is the number of sides of a polygon. for example, to find the sum of interior angles of a pentagon, we will substitute the value of 'n' in the formula: s= (n 2) × 180°; in this case, n = 5. so, (5 2) × 180° = 3 × 180°= 540°. Let us discuss the three different formulas in detail. method 1: if “n” is the number of sides of a polygon, then the formula is given below: interior angles of a regular polygon = [180° (n) – 360°] n. method 2: if the exterior angle of a polygon is given, then the formula to find the interior angle is.
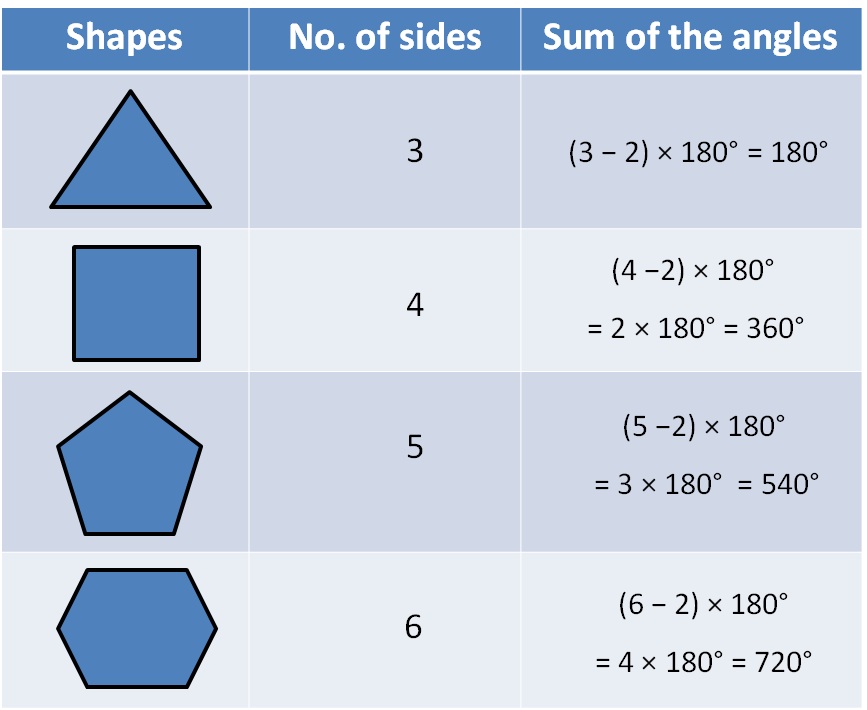
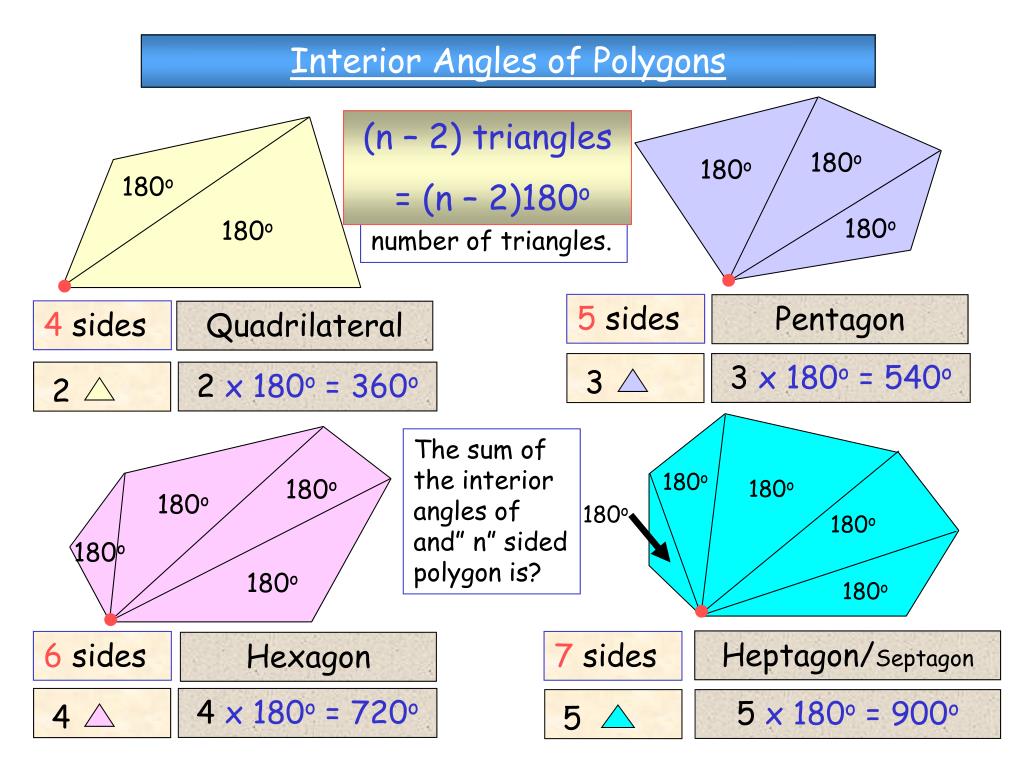
Angle Sum Property Of Polygons With Formula Teachoo Polygons The sum of all interior angles of a regular polygon is calculated by the formula s= (n 2) × 180°, where 'n' is the number of sides of a polygon. for example, to find the sum of interior angles of a pentagon, we will substitute the value of 'n' in the formula: s= (n 2) × 180°; in this case, n = 5. so, (5 2) × 180° = 3 × 180°= 540°. Let us discuss the three different formulas in detail. method 1: if “n” is the number of sides of a polygon, then the formula is given below: interior angles of a regular polygon = [180° (n) – 360°] n. method 2: if the exterior angle of a polygon is given, then the formula to find the interior angle is. To calculate the sum of interior angles of a polygon, you need its number of sides. mathematically, the sum of the angles is expressed as: sum of interior angles of a polygon \(=(n 2)\times 180^{\circ}\) where, n is the number of sides of the polygon the angle is measured in degrees. Scroll down the page for more examples and solutions on the interior angles of a polygon. example: find the sum of the interior angles of a heptagon (7 sided) solution: step 1: write down the formula (n 2) × 180°. step 2: plug in the values to get (7 2) × 180° = 5 × 180° = 900°. answer: the sum of the interior angles of a heptagon (7.

Sum Of Interior Angles Solve For X Youtube To calculate the sum of interior angles of a polygon, you need its number of sides. mathematically, the sum of the angles is expressed as: sum of interior angles of a polygon \(=(n 2)\times 180^{\circ}\) where, n is the number of sides of the polygon the angle is measured in degrees. Scroll down the page for more examples and solutions on the interior angles of a polygon. example: find the sum of the interior angles of a heptagon (7 sided) solution: step 1: write down the formula (n 2) × 180°. step 2: plug in the values to get (7 2) × 180° = 5 × 180° = 900°. answer: the sum of the interior angles of a heptagon (7.
Sum Of Interior And Exterior Angles Of Polygons

Comments are closed.