How To Find The Derivative Using Chain Rule

Chain Rule For Finding Derivatives Youtube However, using all of those techniques to break down a function into simpler parts that we are able to differentiate can get cumbersome. instead, we use the chain rule, which states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function times the derivative of the inner function. To do the chain rule: differentiate the outer function, keeping the inner function the same. multiply this by the derivative of the inner function. for example, differentiate (4𝑥 – 3) 5 using the chain rule. in this example we will use the chain rule step by step. below this, we will use the chain rule formula method.

Chain Rule Theorem Proof Examples Chain Rule Derivative This calculus video tutorial explains how to find derivatives using the chain rule. this lesson contains plenty of practice problems including examples of c. Worked example. let’s now take a look at a problem to see the chain rule in action as we find the derivative of the following function: chain rule — examples. see, all we did was first take the derivative of the outside function (parentheses), keeping the inside as is. next, we multiplied by the derivative of the inside function, and lastly. Use the chain rule to find $$\displaystyle \frac d {dx}\left(\sec x\right)$$. step 1. rewrite the function in terms of the cosine. $$ \sec x = \frac 1 {\cos x} = \big(\cos x\big)^{ 1} $$ step 2. differentiate using the chain rule. Example 60: using the chain rule. use the chain rule to find the derivatives of the following functions, as given in example 59. solution. example 59 ended with the recognition that each of the given functions was actually a composition of functions. to avoid confusion, we ignore most of the subscripts here. \(f 1(x) = (1 x)^2\):.

Chain Rule For Derivatives Explained With Examples Youtube Use the chain rule to find $$\displaystyle \frac d {dx}\left(\sec x\right)$$. step 1. rewrite the function in terms of the cosine. $$ \sec x = \frac 1 {\cos x} = \big(\cos x\big)^{ 1} $$ step 2. differentiate using the chain rule. Example 60: using the chain rule. use the chain rule to find the derivatives of the following functions, as given in example 59. solution. example 59 ended with the recognition that each of the given functions was actually a composition of functions. to avoid confusion, we ignore most of the subscripts here. \(f 1(x) = (1 x)^2\):. The derivative tells us the slope of a function at any point. there are rules we can follow to find many derivatives. for example: the slope of a constant value (like 3) is always 0; the slope of a line like 2x is 2, or 3x is 3 etc; and so on. if we know the rate of change for two related things, how do we work out the overall rate of change?. This calculus video tutorial explains how to find the derivative of a multiple composite function using the chain rule.derivatives fast review:.
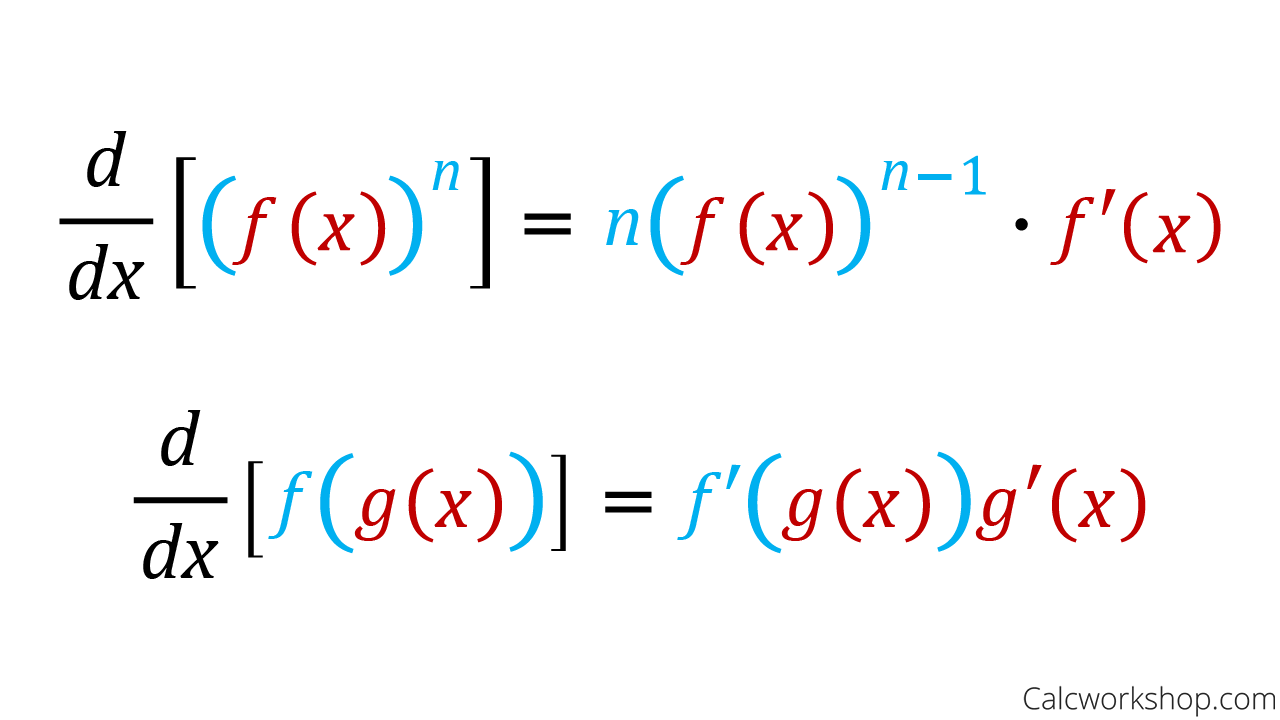
Chain Rule Explained W 7 Step By Step Examples The derivative tells us the slope of a function at any point. there are rules we can follow to find many derivatives. for example: the slope of a constant value (like 3) is always 0; the slope of a line like 2x is 2, or 3x is 3 etc; and so on. if we know the rate of change for two related things, how do we work out the overall rate of change?. This calculus video tutorial explains how to find the derivative of a multiple composite function using the chain rule.derivatives fast review:.

Comments are closed.