How To Draw The Golden Ratio Correctly

How To Draw The Golden Ratio Correctly Youtube This video describe how to draw golden ratio step by step. The golden ratio is a number that’s (kind of) equal to 1.618, just like pi is approximately equal to 3.14, but not exactly. you take a line and divide it into two parts – a long part (a) and a short part (b). the entire length (a b) divided by (a) is equal to (a) divided by (b). and both of those numbers equal 1.618.

How To Draw A Golden Ratio Rectangle Spiral Sacred Geometry The golden ratio. applying the golden ratio to art means placing the main subjects along intersecting lines, as you’d do when using the rule of thirds. the “phi grid” is similar to the rule of thirds layout but the parallel lines are closer to the center. this results in nine boxes that are not uniform in size. Step 1 – construct a simple square. step 2 – draw a line down the middle of the square. step 3 – grab your compass and place one point at the intersection at the bottom middle and draw down from the edge of top right corner, as shown below. step 4 – complete the golden rectangle. Approximately equal to a 1:1.61 ratio, the golden ratio can be illustrated using a golden rectangle. this is a rectangle where, if you cut off a square (side length equal to the shortest side of the rectangle), the rectangle that's left will have the same proportions as the original rectangle. a golden rectangle. Draw a quarter circle in each square, touching at the corners. the resulting spiral approximates the golden spiral, a form of the golden ratio. using a graphic software. open your graphic software.
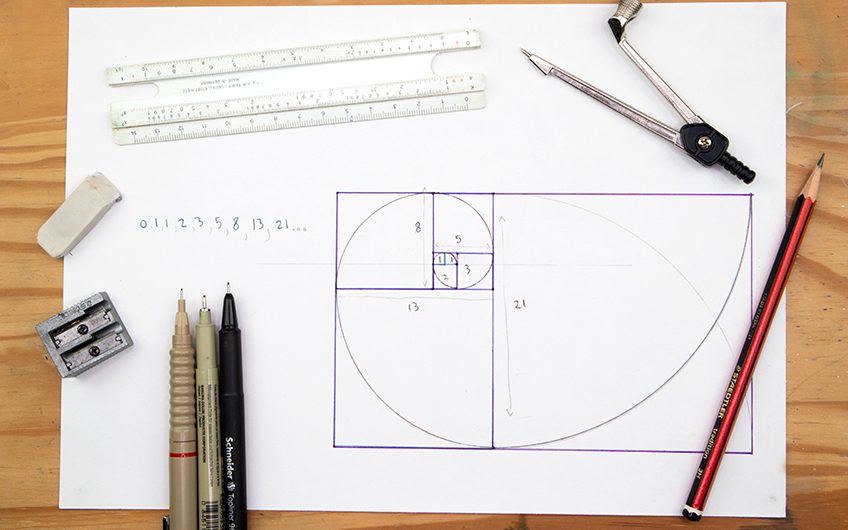
How To Draw The Golden Ratio Approximately equal to a 1:1.61 ratio, the golden ratio can be illustrated using a golden rectangle. this is a rectangle where, if you cut off a square (side length equal to the shortest side of the rectangle), the rectangle that's left will have the same proportions as the original rectangle. a golden rectangle. Draw a quarter circle in each square, touching at the corners. the resulting spiral approximates the golden spiral, a form of the golden ratio. using a graphic software. open your graphic software. The golden ratio is a mathematical proportion defined by the ratio of 1 to 1.618, represented by the greek letter phi. it is an irrational number, meaning its value cannot be expressed exactly as a simple fraction. the golden ratio is also called the golden section, golden mean, divine proportion, extreme and mean ratio, and the divine proportion. The golden ratio, also known as “phi” and more popularly known as the fibonacci sequence, is an irregular equation. a ratio of 1 to 1.618 is what is referred to as an irrational number, similar to that of the famous einstein equation “pi”. for the sake of beautiful aesthetics, this ratio can be a helpful tool for capturing balance and.

How To Draw A Golden Ratio Spiral Youtube The golden ratio is a mathematical proportion defined by the ratio of 1 to 1.618, represented by the greek letter phi. it is an irrational number, meaning its value cannot be expressed exactly as a simple fraction. the golden ratio is also called the golden section, golden mean, divine proportion, extreme and mean ratio, and the divine proportion. The golden ratio, also known as “phi” and more popularly known as the fibonacci sequence, is an irregular equation. a ratio of 1 to 1.618 is what is referred to as an irrational number, similar to that of the famous einstein equation “pi”. for the sake of beautiful aesthetics, this ratio can be a helpful tool for capturing balance and.

How To Draw Golden Ratio Artofit

Comments are closed.