How To Derive The Best Slope And Intercept In A Simple Linear Regression

How To Derive The Best Slope And Intercept In A Simple Linear Linear regression equation. linear regression line equation is written in the form: y = a bx. where, x is independent variable, plotted along x axis. y is dependent variable, plotted along y axis. the slope of the regression line is “b”, and the intercept value of regression line is “a” (the value of y when x = 0). Microsoft word 10.simple linear regression.doc. simple linear regression is the most commonly used technique for determining how one variable of interest (the response variable) is affected by changes in another variable (the explanatory variable). the terms "response" and "explanatory" mean the same thing as "dependent" and "independent.

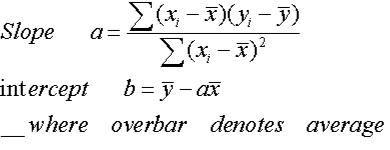
12 Simple Linear Regression Analysis Bia 2200 Resources Simple linear regression is a type of regression that involves one independent variable (explanatory variable) and one dependent variable (response variable). it is used to predict a continuous outcome based on a linear relationship between these two variables. Estimation of regression function •consider the deviation of observed data yi from a straight line with slope aand intercept b, yi−(axi b) it measures how good the line ax bfits the data (xi,yi) in terms of vertical distance •method of least squares (smallest sum of squared derivation) – find the value of aand bwhich minimize q= xn i=1. C plot.9.2 statistical hypothesesfor simple linear regression, the chief null hypothesis is h0 : β1 = 0, and the corresponding alter. ative hypothesis is h1 : β1 6= 0. if this null hypothesis is true, then, from e(y ) = β0 β1x we can see that the population mean of y is β0 for every x value, which t. An alternative way of estimating the simple linear regression model starts from the objective we are trying to reach, rather than from the formula for the slope. recall, from lecture 1, that the true optimal slope and intercept are the ones which minimize the mean squared error: ( 0; 1) = argmin (b 0;b 1) e (y (b 0 b 1x))2 (5).

Intro To Simple Linear Regression Slope Y Intercept R Square Youtube C plot.9.2 statistical hypothesesfor simple linear regression, the chief null hypothesis is h0 : β1 = 0, and the corresponding alter. ative hypothesis is h1 : β1 6= 0. if this null hypothesis is true, then, from e(y ) = β0 β1x we can see that the population mean of y is β0 for every x value, which t. An alternative way of estimating the simple linear regression model starts from the objective we are trying to reach, rather than from the formula for the slope. recall, from lecture 1, that the true optimal slope and intercept are the ones which minimize the mean squared error: ( 0; 1) = argmin (b 0;b 1) e (y (b 0 b 1x))2 (5). Machine learning example with python: simple linear regression in this machine learning example we are going to see a linear regression with only one input feature. a simple linear regression. The formula for a simple linear regression is: y is the predicted value of the dependent variable (y) for any given value of the independent variable (x). b0 is the intercept, the predicted value of y when the x is 0. b1 is the regression coefficient – how much we expect y to change as x increases. x is the independent variable ( the variable.

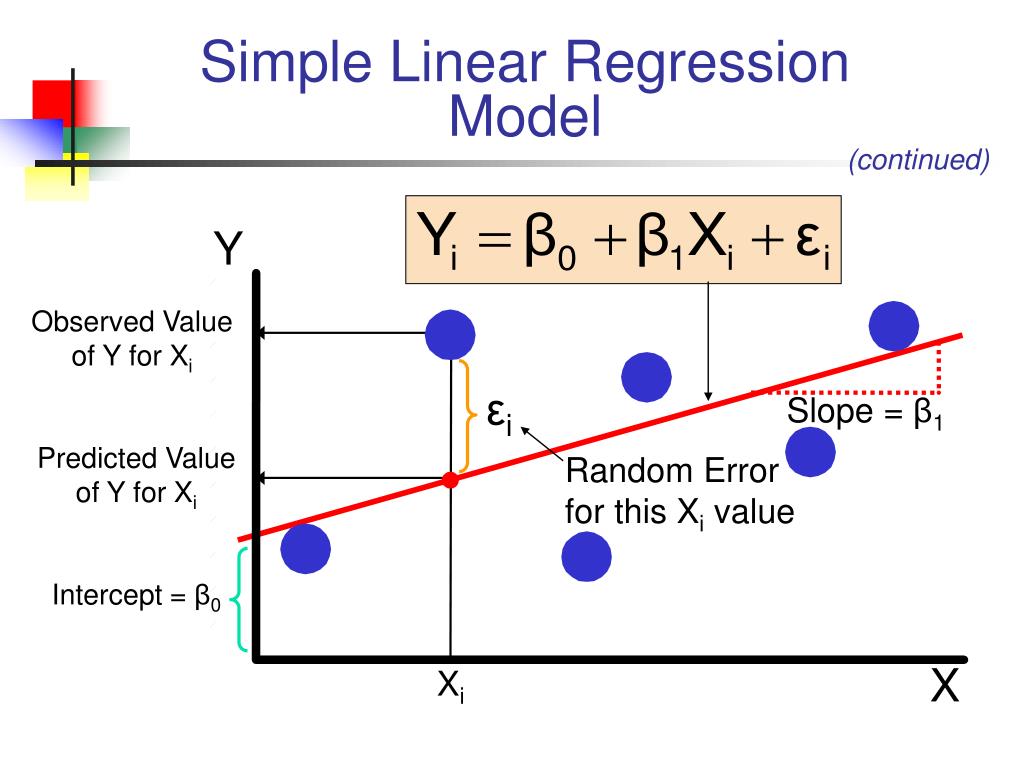
Ppt Chapter 11 Simple Linear Regression Analysis 线性回归分析 Machine learning example with python: simple linear regression in this machine learning example we are going to see a linear regression with only one input feature. a simple linear regression. The formula for a simple linear regression is: y is the predicted value of the dependent variable (y) for any given value of the independent variable (x). b0 is the intercept, the predicted value of y when the x is 0. b1 is the regression coefficient – how much we expect y to change as x increases. x is the independent variable ( the variable.