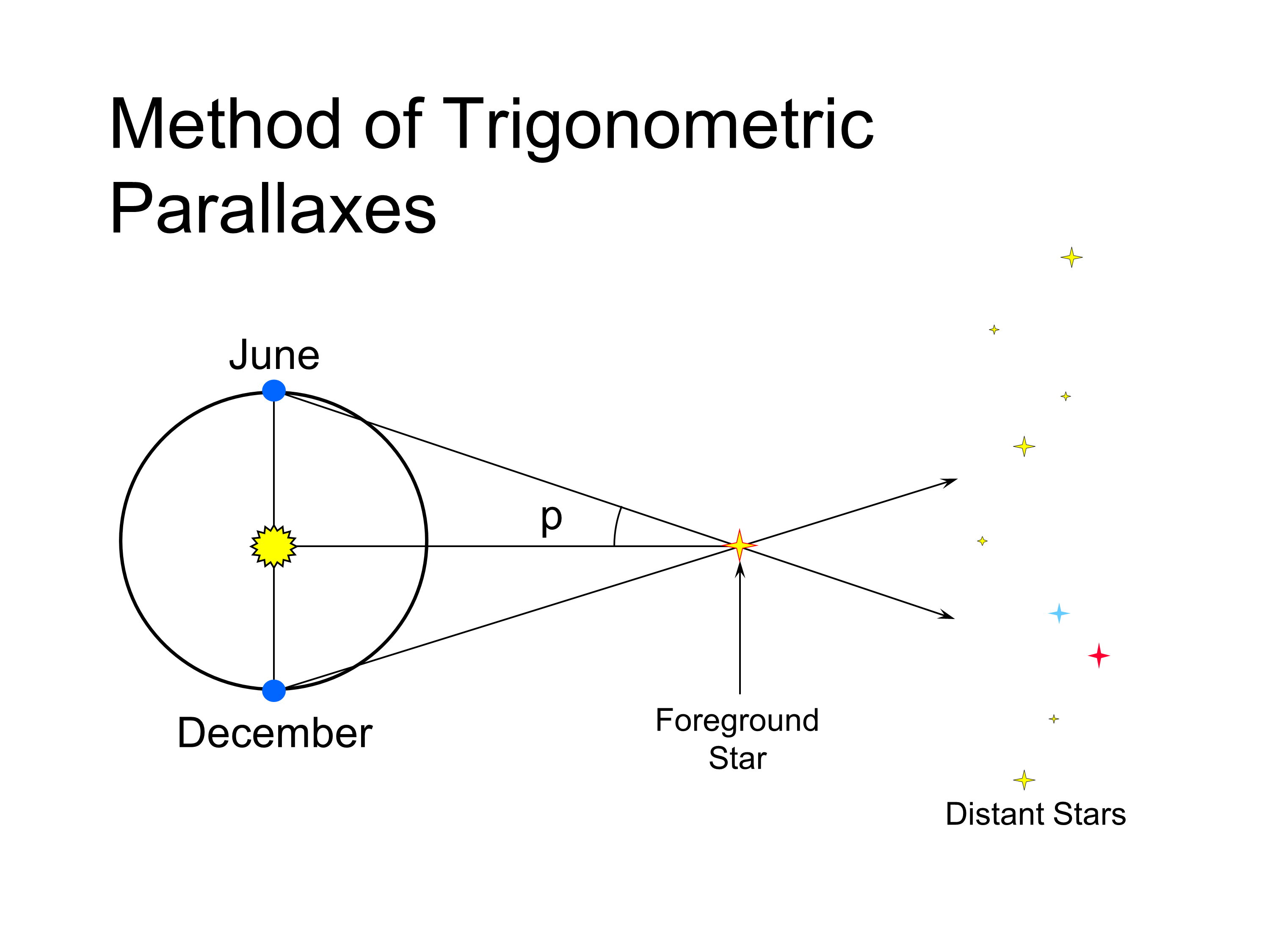
Lecture 5 Stellar Distances Published 11 january 2022. parallax is the observed displacement of an object caused by the change of the observer's point of view. in astronomy, it is an irreplaceable tool for calculating. A distance of one parsec is de ned as the distance at which an object has a parallax of one arc second. this is an angle of: (radians) = 1:0au 1:0parsec converting to arc seconds: (arcseconds) = 1:0au 1:0parsec 360 2ˇ 60 60 = 1:0au 1:0parsec 206265 so 1 parsec = 206,265 au. it is also about 3.26 light years. 5 36.
What Is The Parallax Formula And How Is It Used To Calculate The The change in a star's position in the sky as a result of its true motion through space is called proper motion. this is distinguished from the annual apparent motion in the sky caused by the earth's orbit around the sun. this apparent motion permits distance measurement by parallax. the largest proper motion is exhibited by barnard's star. In the example of the thumb raised to arm height, we can derive the distance between the thumb and the face if we know a) the parallax angle formed by the shift of the thumb observed alternately. Parallax decreases with distance. as the distance to a star increases, the its parallax decreases. this is easy to see in the following two figures: (click on the image to view at full scale [size: 165kb]) in the upper figure, the star is about 2.5 times nearer than the star in the lower figure, and has a parallax angle which is 2.5 times larger. Stellar parallax is most often measured using annual parallax, defined as the difference in position of a star as seen from earth and sun, i.e. the angle subtended at a star by the mean radius of earth's orbit around the sun. the parsec (3.26 light years) is defined as the distance for which the annual parallax is 1 arcsecond. annual parallax.
How To Measure Stellar Distances With The Parallax Method By Michele Parallax decreases with distance. as the distance to a star increases, the its parallax decreases. this is easy to see in the following two figures: (click on the image to view at full scale [size: 165kb]) in the upper figure, the star is about 2.5 times nearer than the star in the lower figure, and has a parallax angle which is 2.5 times larger. Stellar parallax is most often measured using annual parallax, defined as the difference in position of a star as seen from earth and sun, i.e. the angle subtended at a star by the mean radius of earth's orbit around the sun. the parsec (3.26 light years) is defined as the distance for which the annual parallax is 1 arcsecond. annual parallax. The parallax formula for calculating approximate distance is: \quad d = \frac {1} {p} d = p 1. where: d. d d – distance between the star and the earth, measured in parsecs; and. p. p p – parallax angle, measured in arcseconds. using the above parallax equation, we can also define 1 parsec as the distance at which an object has a parallax of. Consider the star α canis major, also known as sirius, the brightest star in the night sky. sirius has a parallax of 0.37921 arcseconds. to calculate the distance, in terms of light years, we use the equation introduced earlier: d (parsec) = 1 p (arcsecond) distance = 1 0.37921 = 2.637 parsecs.
Comments are closed.