Grouped Discrete Data How To Estimate The Mean With Midpoints Mid Values And Frequency Table

Grouped Discrete Data How To Calculate The Mean With Midpoints Mid For grouped data, we estimate the mean using the midpoints, or mid values, of each of the groups (classes). with the formula each mid value is multiplied by. To calculate the mean for grouped discrete data, we use the midpoints, or mid values, of each of the groups (classes). the sum of the product of each mid val.

How To Calculate The Mean Average Of For Grouped Data From A Frequency The following table shows the frequency distribution of the diameters of 40 bottles. (lengths have been measured to the nearest millimeter) find the mean of the data. step 1: find the midpoint of each interval. step 2: multiply the frequency of each interval by its mid point. step 3: get the sum of all the frequencies (f) and the sum of all the fx. Summary. for grouped data, we cannot find the exact mean, median and mode, we can only give estimates. to estimate the mean use the midpoints of the class intervals: estimated mean = sum of (midpoint × frequency) sum of frequency. to estimate the median use: estimated median = l (n 2) − b g × w. where:. Calculate the standard deviation of grouped data. we can use the following formula to estimate the standard deviation of grouped data: standard deviation: √Σni(mi μ)2 (n 1) where: ni: the frequency of the ith group. mi: the midpoint of the ith group. μ: the mean. n: the total sample size. here’s how we would apply this formula to our. Estimated mean from a grouped frequency table. when the data has been grouped together and put into a grouped frequency table, you cannot find the actual mean because you only have a range of possible values. instead you can find an estimate for the mean using the midpoints of each group. you can add more columns to the grouped frequency table.

Mean From A Frequency Table Gcse Maths Steps Examples Worksheet Calculate the standard deviation of grouped data. we can use the following formula to estimate the standard deviation of grouped data: standard deviation: √Σni(mi μ)2 (n 1) where: ni: the frequency of the ith group. mi: the midpoint of the ith group. μ: the mean. n: the total sample size. here’s how we would apply this formula to our. Estimated mean from a grouped frequency table. when the data has been grouped together and put into a grouped frequency table, you cannot find the actual mean because you only have a range of possible values. instead you can find an estimate for the mean using the midpoints of each group. you can add more columns to the grouped frequency table. We can calculate an estimate for the mean of a grouped frequency table by following the steps below: find the midpoint, 𝑥, of each group in the table by adding the boundary values and dividing by 2. multiply the midpoints by the frequencies, 𝐹, of the corresponding classes to give 𝐹 𝑥. Estimated mean from a grouped frequency table. when the data has been grouped together and put into a grouped frequency table we cannot find the actual mean because we only have a range of possible values. instead we can find an estimate for the mean using the midpoints of each group. we can add more columns to the grouped frequency table to.

Estimated Means From Grouped Data Video Corbettmaths We can calculate an estimate for the mean of a grouped frequency table by following the steps below: find the midpoint, 𝑥, of each group in the table by adding the boundary values and dividing by 2. multiply the midpoints by the frequencies, 𝐹, of the corresponding classes to give 𝐹 𝑥. Estimated mean from a grouped frequency table. when the data has been grouped together and put into a grouped frequency table we cannot find the actual mean because we only have a range of possible values. instead we can find an estimate for the mean using the midpoints of each group. we can add more columns to the grouped frequency table to.

Mean Of A Grouped Data Igcse At Mathematics Realm

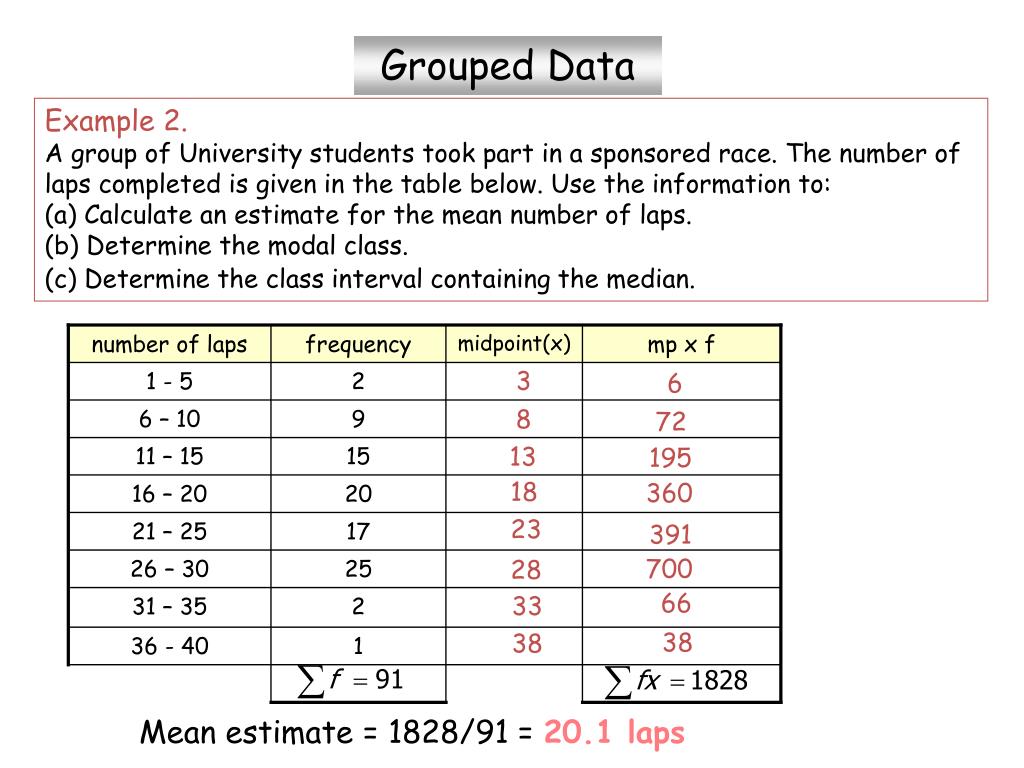
How To Find The Mean Of A Grouped Data Frequency Table Brokeasshome