Graphs Of Polynomial Functions Algebra And Trigonometry
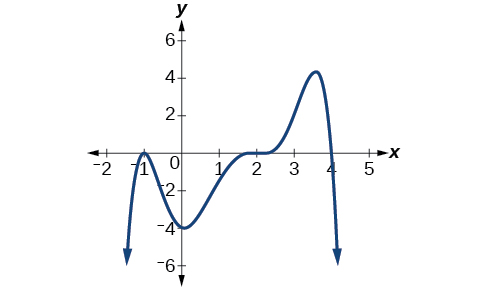
Graphs Of Polynomial Functions Algebra And Trigonometry The graph of a polynomial will touch the horizontal axis at a zero with even multiplicity. the end behavior of a polynomial function depends on the leading term. the graph of a polynomial function changes direction at its turning points. a polynomial function of degree n has at most n − 1 turning points. The graph of a polynomial will touch the horizontal axis at a zero with even multiplicity. the end behavior of a polynomial function depends on the leading term. the graph of a polynomial function changes direction at its turning points. a polynomial function of degree n has at most n − 1 turning points.
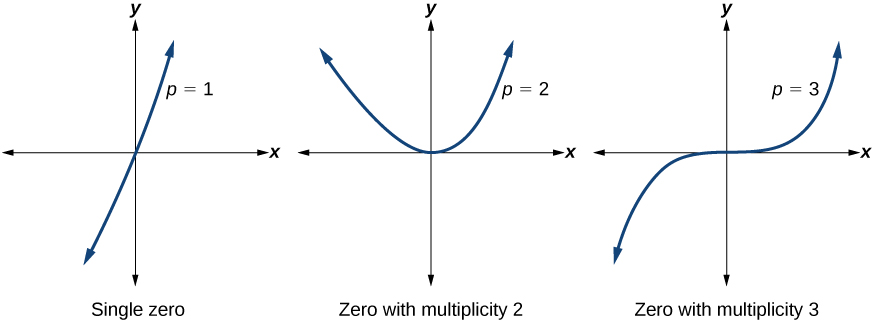
Graphs Of Polynomial Functions Algebra And Trigonometry Using factoring to find zeros of polynomial functions. recall that if f f is a polynomial function, the values of x x for which f (x) = 0 f (x) = 0 are called zeros of f. f. if the equation of the polynomial function can be factored, we can set each factor equal to zero and solve for the zeros. Write a formula for the polynomial function shown in figure 5.3.20. figure 5.3.20. solution. this graph has three x intercepts: x = − 3, 2, and 5. the y intercept is located at (0, 2).at x = − 3 and x = 5, the graph passes through the axis linearly, suggesting the corresponding factors of the polynomial will be linear. It may have a turning point where the graph changes from increasing to decreasing (rising to falling) or decreasing to increasing (falling to rising). look at the graph of the polynomial function f(x) = x4 −x3 − 4x2 4x in figure 12. the graph has three turning points. figure 12. Speaking of intercepts, we next focus our attention on the behavior of the graphs of polynomial functions near their zeros. recall a zero of a function is a solution to . geometrically, the zeros of a function are the coordinates of the intercepts of the graph of . consider the polynomial function . to find the zeros of , we set .
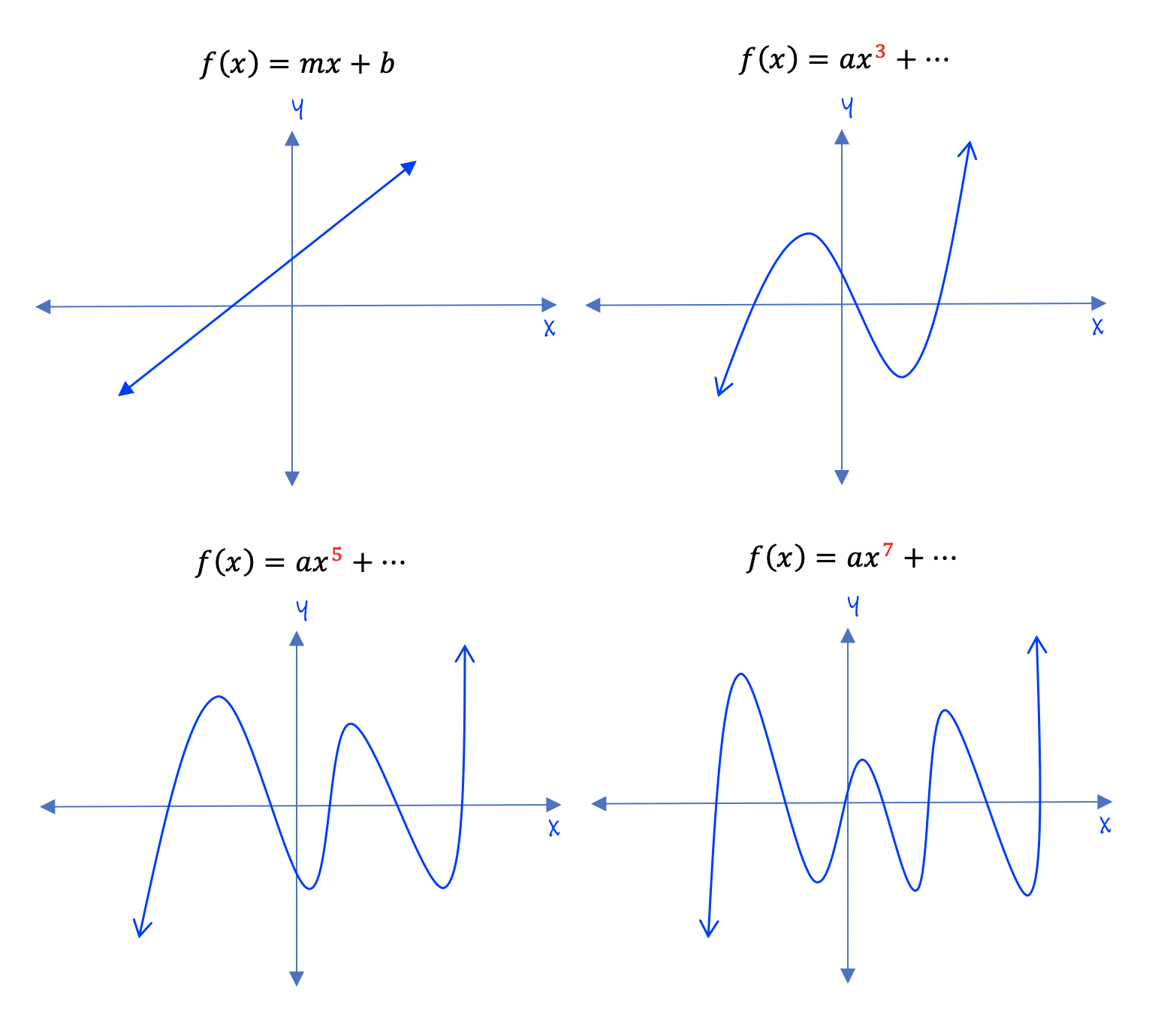
Graphs Of Polynomial Functions It may have a turning point where the graph changes from increasing to decreasing (rising to falling) or decreasing to increasing (falling to rising). look at the graph of the polynomial function f(x) = x4 −x3 − 4x2 4x in figure 12. the graph has three turning points. figure 12. Speaking of intercepts, we next focus our attention on the behavior of the graphs of polynomial functions near their zeros. recall a zero of a function is a solution to . geometrically, the zeros of a function are the coordinates of the intercepts of the graph of . consider the polynomial function . to find the zeros of , we set . Answer: the graphs of f and h are graphs of polynomial functions. they are smooth and continuous. the graphs of g and k are graphs of functions that are not polynomials. the graph of function g has a sharp corner. the graph of function k is not continuous. A polynomial function of n th n th degree is the product of n n factors, so it will have at most n n roots or zeros, or x intercepts. the graph of the polynomial function of degree n n must have at most n – 1 n – 1 turning points. this means the graph has at most one fewer turning point than the degree of the polynomial or one fewer than.

Comments are closed.