Golden Ratio History Of Golden Ratio Magic Or Myth Letstute

Golden Ratio History Of Golden Ratio Magic Or Myth Letstute What is the golden ratio?history of the golden ratio?magic or myth? the golden ratio | fibonacciuse of golden ratio the golden ratio: is it myth or math?the. The golden ratio is defined by the formula (a b) a = a b, where “a” is the longer segment, and “b” is the shorter segment. the value of the golden ratio is approximately 1.6180339887, and it is represented by the greek letter phi (φ). the golden ratio and geometry. the golden ratio appears in various geometric constructions.
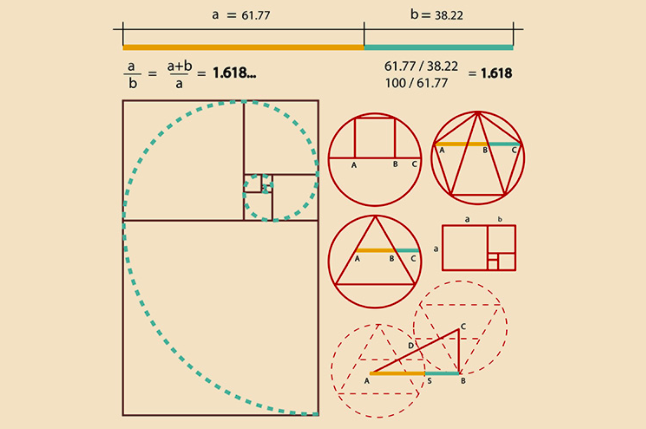
The Golden Ratio Myth Or Magic Of Mathematics Nu Sci Magazine In words: two quantities a and b, with a being the greater one, are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. the ratio can be represented by the irrational number phi, which is a solution to the quadratic equation x2 – x – 1 = 0. from the golden ratio comes the golden. The golden ratio's negative −φ and reciprocal φ−1 are the two roots of the quadratic polynomial x2 x − 1. the golden ratio is also an algebraic number and even an algebraic integer. it has minimal polynomial. this quadratic polynomial has two roots, and. the golden ratio is also closely related to the polynomial. The “golden ratio” was coined in the 1800’s. it is believed that martin ohm (1792–1872) was the first person to use the term “golden” to describe the golden ratio. to use the term. in 1815, he published “ die reine elementar mathematik ” (the pure elementary mathematics). this book is famed for containing the first known usage. If you take a line divided into two segments a and b so that a b is the golden ratio, and then form a rectangle with sides a b and a, then this rectangle is called a golden rectangle. a golden rectangle is made up of a square (white) and a smaller rectangle (grey). the smaller rectangle is also a golden rectangle.

The Myth Of The Golden Ratio Hanttula The “golden ratio” was coined in the 1800’s. it is believed that martin ohm (1792–1872) was the first person to use the term “golden” to describe the golden ratio. to use the term. in 1815, he published “ die reine elementar mathematik ” (the pure elementary mathematics). this book is famed for containing the first known usage. If you take a line divided into two segments a and b so that a b is the golden ratio, and then form a rectangle with sides a b and a, then this rectangle is called a golden rectangle. a golden rectangle is made up of a square (white) and a smaller rectangle (grey). the smaller rectangle is also a golden rectangle. There is one thing that ancient greeks, renaissance artists, a 17th century astronomer and 21st century architects all have in common – they all used the golden mean, otherwise known as the golden ratio, divine proportion, or golden section. precisely, this is the number 1.61803399, represented by the greek letter phi, and considered truly. The golden ratio has been famed throughout history for its aesthetic properties and it is claimed that the architecture of ancient greece was strongly influenced by its use. the article [ 11 ] discusses whether the golden section is a universal natural phenomenon, to what extent it has been used by architects and painters, and whether there is.

Ppt The Golden Ratio Powerpoint Presentation Free Download Id 1744363 There is one thing that ancient greeks, renaissance artists, a 17th century astronomer and 21st century architects all have in common – they all used the golden mean, otherwise known as the golden ratio, divine proportion, or golden section. precisely, this is the number 1.61803399, represented by the greek letter phi, and considered truly. The golden ratio has been famed throughout history for its aesthetic properties and it is claimed that the architecture of ancient greece was strongly influenced by its use. the article [ 11 ] discusses whether the golden section is a universal natural phenomenon, to what extent it has been used by architects and painters, and whether there is.

Comments are closed.