Golden Ratio Definition Formula Examples

Golden Ratio Definition Formula Examples Golden ratio. golden ratio, golden mean, golden section, or divine proportion refers to the ratio between two quantities such that the ratio of their sum to the larger of the two quantities is approximately equal to 1.618. it is denoted by the symbol ‘ϕ’ (phi), an irrational number because it never terminates and never repeats. The golden ratio formula can be used to calculate the value of the golden ratio. the golden ratio equation is derived to find the general formula to calculate golden ratio. golden ratio equation. from the definition of the golden ratio, a b = (a b) a = ϕ. from this equation, we get two equations: a b = ϕ → (1) (a b) a = ϕ → (2) from.

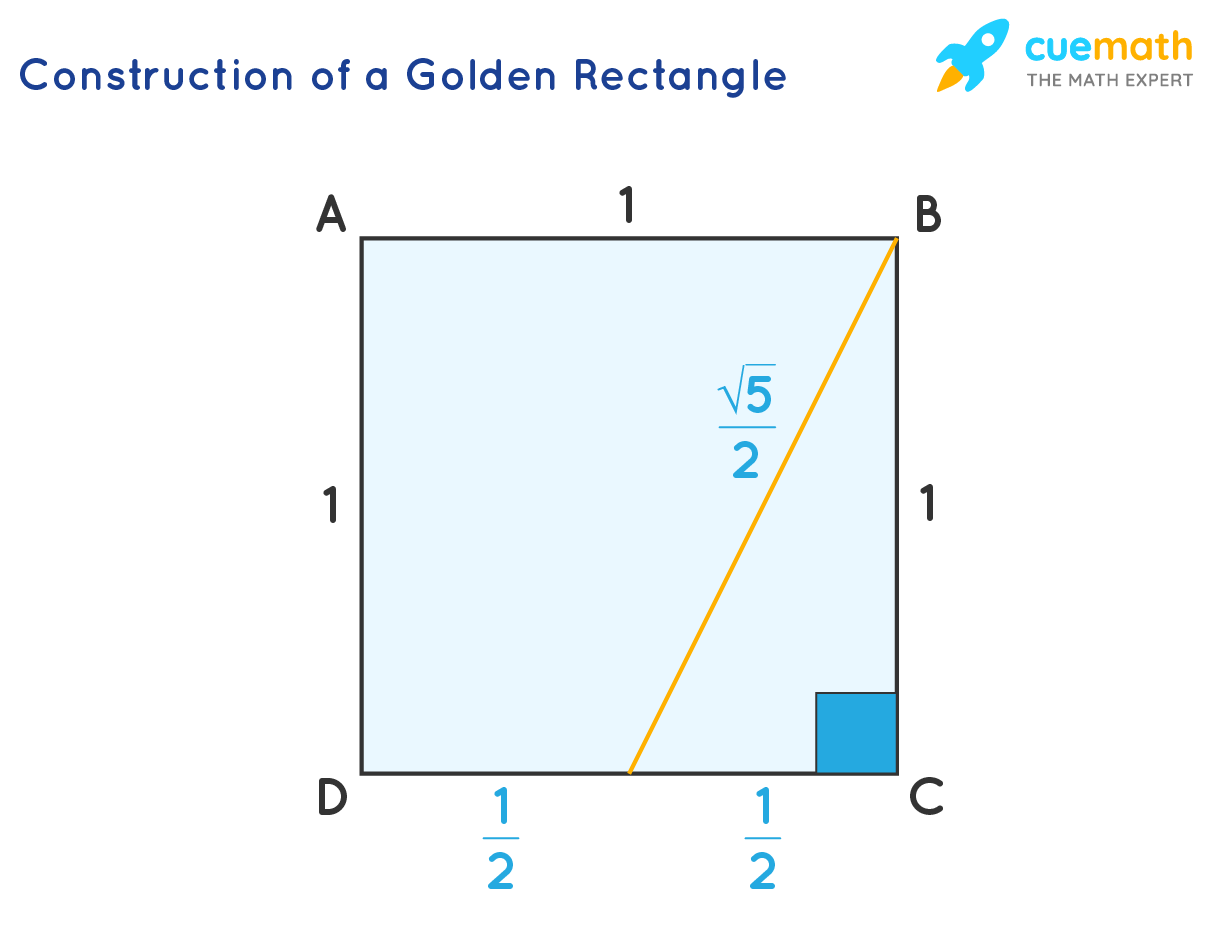
Golden Ratio Definition Formula Examples Golden ratio is a special number and is approximately equal to 1.618. golden ratio is represented using the symbol “ϕ”. golden ratio formula is ϕ = 1 (1 ϕ). ϕ is also equal to 2 × sin (54°) if we take any two successive fibonacci numbers, their ratio is very close to the value 1.618 (golden ratio). A quick way to calculate. that rectangle above shows us a simple formula for the golden ratio. when the short side is 1, the long side is 1 2 √5 2, so: the square root of 5 is approximately 2.236068, so the golden ratio is approximately 0.5 2.236068 2 = 1.618034. this is an easy way to calculate it when you need it. Golden rectangle. golden ratio, in mathematics, the irrational number (1 square root of√5) 2, often denoted by the greek letter ϕ or τ, which is approximately equal to 1.618. it is the ratio of a line segment cut into two pieces of different lengths such that the ratio of the whole segment to that of the longer segment is equal to the. The golden ratio is also an algebraic number and even an algebraic integer. it has minimal polynomial. this quadratic polynomial has two roots, and. the golden ratio is also closely related to the polynomial. which has roots and as the root of a quadratic polynomial, the golden ratio is a constructible number.

Golden Ratio Definition Formula Examples Golden rectangle. golden ratio, in mathematics, the irrational number (1 square root of√5) 2, often denoted by the greek letter ϕ or τ, which is approximately equal to 1.618. it is the ratio of a line segment cut into two pieces of different lengths such that the ratio of the whole segment to that of the longer segment is equal to the. The golden ratio is also an algebraic number and even an algebraic integer. it has minimal polynomial. this quadratic polynomial has two roots, and. the golden ratio is also closely related to the polynomial. which has roots and as the root of a quadratic polynomial, the golden ratio is a constructible number. Golden ratio explained: how to calculate the golden ratio. written by masterclass. last updated: jun 7, 2021 • 2 min read. the golden ratio is a famous mathematical concept that is closely tied to the fibonacci sequence. The golden ratio is a special ratio with approximate value 1.61803 , an irrational number. the golden ratio is typically denoted with the greek letter, phi (φ), and has been studied by mathematicians throughout history, including euclid (~300 bc). in definition, two values exhibit the golden ratio if the ratio of the sum of the two values to.