Geometry Transitive Property Angles This geometry video tutorial provides a basic introduction into two column proofs with angles. it covers the addition and subtraction property of equality a. A proof is a logical argument that uses deductive reasoning to show that a statement is true. there are several formats for proofs. a two column proof has numbered statements and corresponding reasons that show an argument in a logical order. in a two column proof, each statement in the left hand column is either given information or the result.
Geometry Two Column Proofs Of Angles Addition Substitution M∠dba = 1 2 3. substitution property of equality 4. m ∠1 2 = m ebc 4. angle addition postulate 5. m ∠dba = m ebc 5. transitive property of equality writing two column proofs a proof is a logical argument that uses deductive reasoning to show that a statement is true. there are several formats for proofs. a. A two column proof has numbered statements and corresponding reasons that show an argument in logical order. theorem. a theorem is a statement that can be proven. writing a two column proof is a. example 1 formal way of organizing your write a two column proof reasons to show a statement is true. use the diagram to prove m∠1 = m∠4. Addition property of equality by showing that adding the measure of ?2 to two equal angles preserves equality. then, by the angle addition postulate we see that ?ptr is the sum of ?1 and ?2, whereas ?stq is the sum of ?3 and ?2. ultimately, through substitution, it is clear that the measures of ?ptr and ?stq are equal. the two column proof for. Statement #1: the given information is shown. statement #2: this statement is used to show that congruent angles are equal in measure. statement #3: in an earlier unit, we examined angle addition. when two angles share a common ray and they are non overlapping angles, then they may be combined as one angle.
Two Column Proof Guide W 7 Step By Step Examples Addition property of equality by showing that adding the measure of ?2 to two equal angles preserves equality. then, by the angle addition postulate we see that ?ptr is the sum of ?1 and ?2, whereas ?stq is the sum of ?3 and ?2. ultimately, through substitution, it is clear that the measures of ?ptr and ?stq are equal. the two column proof for. Statement #1: the given information is shown. statement #2: this statement is used to show that congruent angles are equal in measure. statement #3: in an earlier unit, we examined angle addition. when two angles share a common ray and they are non overlapping angles, then they may be combined as one angle. In geometry those statements are postulates and definitions. we also depend on a list of undefined terms. statements that are proved relying on undefined terms are called theorems. once a theorem is proved, it may be used as a tool to prove other statements. theorem 2 1: congruence of segments is reflexive, symmetric and transitive. Two column proofs. a two column proof is one common way to organize a proof in geometry. two column proofs always have two columns: one for statements and one for reasons. the best way to understand two column proofs is to read through examples. when writing your own two column proof, keep these things in mind: number each step.
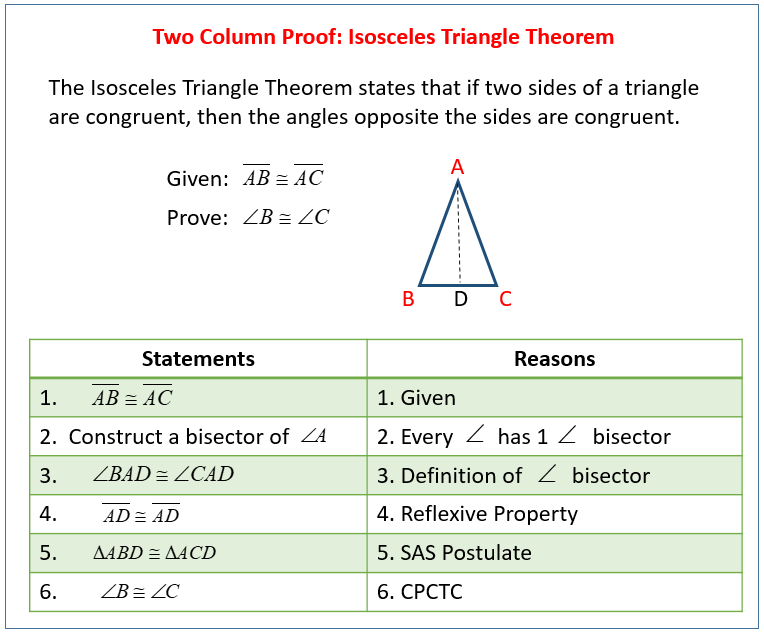
Two Column Proofs Video Lessons Examples Solutions In geometry those statements are postulates and definitions. we also depend on a list of undefined terms. statements that are proved relying on undefined terms are called theorems. once a theorem is proved, it may be used as a tool to prove other statements. theorem 2 1: congruence of segments is reflexive, symmetric and transitive. Two column proofs. a two column proof is one common way to organize a proof in geometry. two column proofs always have two columns: one for statements and one for reasons. the best way to understand two column proofs is to read through examples. when writing your own two column proof, keep these things in mind: number each step.
Angle Properties Postulates And Theorems Wyzant Lessons
Comments are closed.