Geometry Circles Measuring Central Angles And Arcs Foldable By

Geometry Circles Measuring Central Angles And Arcs Foldable By 44. products. $47.52 $66.00 save $18.48. view bundle. geometry circles bundle. this is a bundle of resources from the chapter in geometry of circles, and contains foldables for the lessons:circles and circumferencemeasures of arcs and anglesarc lengtharcs and chordsinscribed anglestangentssecants & tangents intercepting inside and on the. There are three parts to this arcs in circles lesson. this lesson includes:vocabulary a half page is included for students to fill in arcs in circles vocabulary. the words included are central angle, arc, minor arc, major arc, and semicircle.foldable there are three flaps. the flaps are finding arc measures, arc addition p.

Geometry Circles Measuring Central Angles And Arcs Foldable By Circles: central angles and arc measures arc length geometry. Circles geometry interactive notebook: central & inscribed angles. after tangents and chords, we move on to angles. we start with a definition and practice for central angles, and then move on to inscribed angles. we use practice problems to develop the theorems for inscribed angles that intercept the same arc, and angles inscribed in semicircles. • a central angle is twice the measurement of an inscribed angle which contains the same arc. conversely, an inscribed angle is one half the measure of a central angle that contains a common arc. • when the inscribed anle is shared by a diameter of the circle, the inscribed angle is equal to 90 degrees. key ideas: step 5. Angles with vertex inside the circle and their arcs. the measure of an angle with its vertex inside the circle is half the sum of the intercepted arcs. the formula is. measure of angle with vertex inside circle = 1 2 × (sum of intercepted arcs) example: find the value of x. solution: 1 2 × (160° 35°) = 97.5°. angle with vertex inside the.

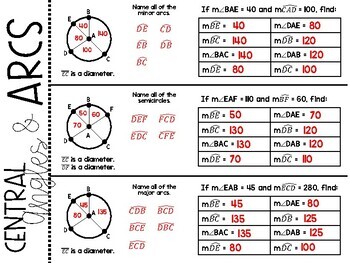
Geometry Circles Measuring Central Angles And Arcs Foldable By • a central angle is twice the measurement of an inscribed angle which contains the same arc. conversely, an inscribed angle is one half the measure of a central angle that contains a common arc. • when the inscribed anle is shared by a diameter of the circle, the inscribed angle is equal to 90 degrees. key ideas: step 5. Angles with vertex inside the circle and their arcs. the measure of an angle with its vertex inside the circle is half the sum of the intercepted arcs. the formula is. measure of angle with vertex inside circle = 1 2 × (sum of intercepted arcs) example: find the value of x. solution: 1 2 × (160° 35°) = 97.5°. angle with vertex inside the. This relationship will be demonstrated by viewing the examples below. example 1. determine the measure of minor arc fw within the diagram that follows. as can be seen within the diagram above, central angle few is 140 degrees. this means the arc it intercepts, arc fw, is equal to the same measure, which is 140 degrees. This was the first lesson in my circles unit, so i needed to introduce some vocabulary first. i gave my students a fill in the blank page with diagrams so that we could discuss the vocabulary as we went. after that, we talked about arc measures, the arc addition postulate, and congruent angles and arcs. i compiled it all into one foldable.

Central Angles And Arcs In Circles Foldable With Graphic Organizer This relationship will be demonstrated by viewing the examples below. example 1. determine the measure of minor arc fw within the diagram that follows. as can be seen within the diagram above, central angle few is 140 degrees. this means the arc it intercepts, arc fw, is equal to the same measure, which is 140 degrees. This was the first lesson in my circles unit, so i needed to introduce some vocabulary first. i gave my students a fill in the blank page with diagrams so that we could discuss the vocabulary as we went. after that, we talked about arc measures, the arc addition postulate, and congruent angles and arcs. i compiled it all into one foldable.