Forming And Solving First Order Differential Equations Notes 1 Doc

Forming And Solving First Order Differential Equations Notes 1 Doc 1 1.5 2 3. separable equations even rst order odes are complicated enough that exact solutions are not easy to obtain in general .one type that can be solved exactly is a separable equation, which is a rst order ode of the form f(y) dy dx = g(x) (3.1) for functions f;g. this can be integrated directly, if you recall the chain rule d dx (f(y(x. The differential equation for the problem can be expressed in a slightly different form from a first order differential equation in (7.24) to be: dt ( x ) q q for the copper wire. dx k 3 . 95. cu. q. the solution of the above differential equation is: t ( x ) x c where c=integration constant.

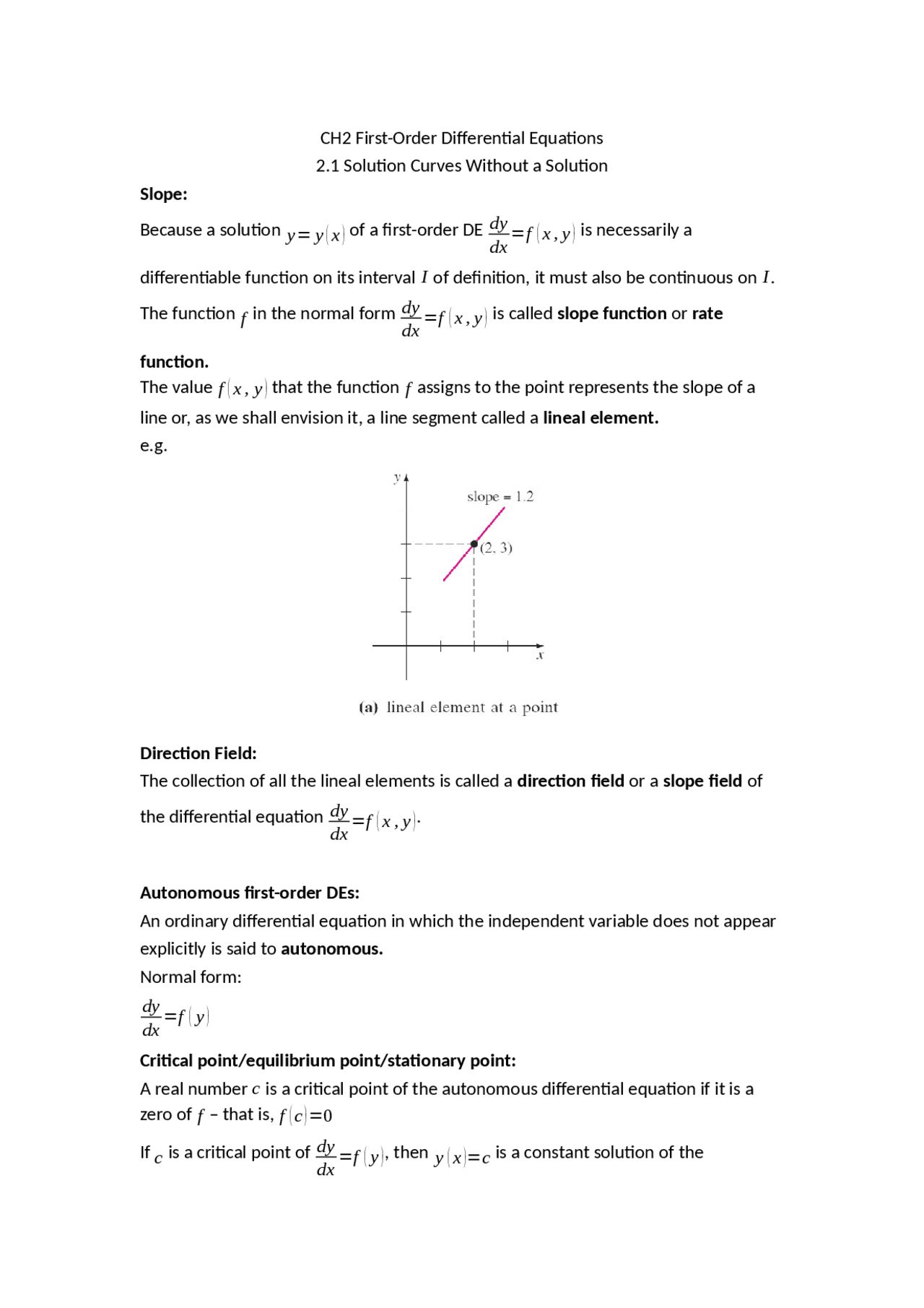
Ch2 First Order Differential Equations Docsity Our study of first order differential equations requires an additional assumption, namely that the equation can be solved for y0. this means that we can write the equation in the form y0 = f(x,y). (f) 2.1. linear differential equations a first order differential equation y0 = f(x,y) is a linear equation if the function f is a “linear. First order linear odes recall that a first order linear ode has the form a 1(x) dy dx a 0(x)y = g(x): (1) definition a first order linear ode (of the above form (1)) is called homogeneous if g(x) = 0 and non homogeneous otherwise. definition by dividing both sides of equation (1) by the leading coefficient a 1(x), we obtain a more. Nisarg amin. follow. 1) first order ordinary linear differential equations can be expressed in the form dy dx = p (x)y q (x), where p and q are functions of x. 2) there are several types of first order linear differential equations, including separable, homogeneous, exact, and linear equations. 3) separable equations can be solved by. A first order equation is separable if it can be written the form. dy dx = f(x)g(y) special cases result when either f(x) = 1 or g(y) = 1. in the first case the equation is said to be autonomous. separable equations. the general solution to equation 1.2.1 is obtained in terms of two integrals:.

1 First Order Odes Lecture Notes 1 Ma31002 Differential Equations Nisarg amin. follow. 1) first order ordinary linear differential equations can be expressed in the form dy dx = p (x)y q (x), where p and q are functions of x. 2) there are several types of first order linear differential equations, including separable, homogeneous, exact, and linear equations. 3) separable equations can be solved by. A first order equation is separable if it can be written the form. dy dx = f(x)g(y) special cases result when either f(x) = 1 or g(y) = 1. in the first case the equation is said to be autonomous. separable equations. the general solution to equation 1.2.1 is obtained in terms of two integrals:. Using first order ode’s. second review of the steps in solving an applied math problem. applied mathematics problem #1: radio active decay. applied mathematics problem #2: continuous compounding. applied mathematics problem #3: mixing (tank) problemsa. applied mathematic problem #4: one dimensional motion of a point particle handout #1. The most general first order differential equation can be written as, dy dt = f (y,t) (1) (1) d y d t = f (y, t) as we will see in this chapter there is no general formula for the solution to (1) (1). what we will do instead is look at several special cases and see how to solve those. we will also look at some of the theory behind first order.

Chapter 7 Solving First Order Differential Equation Numerically Using first order ode’s. second review of the steps in solving an applied math problem. applied mathematics problem #1: radio active decay. applied mathematics problem #2: continuous compounding. applied mathematics problem #3: mixing (tank) problemsa. applied mathematic problem #4: one dimensional motion of a point particle handout #1. The most general first order differential equation can be written as, dy dt = f (y,t) (1) (1) d y d t = f (y, t) as we will see in this chapter there is no general formula for the solution to (1) (1). what we will do instead is look at several special cases and see how to solve those. we will also look at some of the theory behind first order.