First Derivative Equations Of Tangents And Normals Further Maths

First Derivative Equations Of Tangents And Normals Further Maths When given a curve, you can find the equation of the normal to the curve at the point by: finding the derivative (gradient) of the curve at point. this is also the gradient of the tangent line. you can find this by differentiating the equation of the curve, and substituting in. extra step: find the negative reciprocal of the gradient. Click here for answers. practice questions. previous: fm gradient of a curve questions. next: fm second derivative questions. the corbettmaths practice questions on equation of a tangent for level 2 further maths.

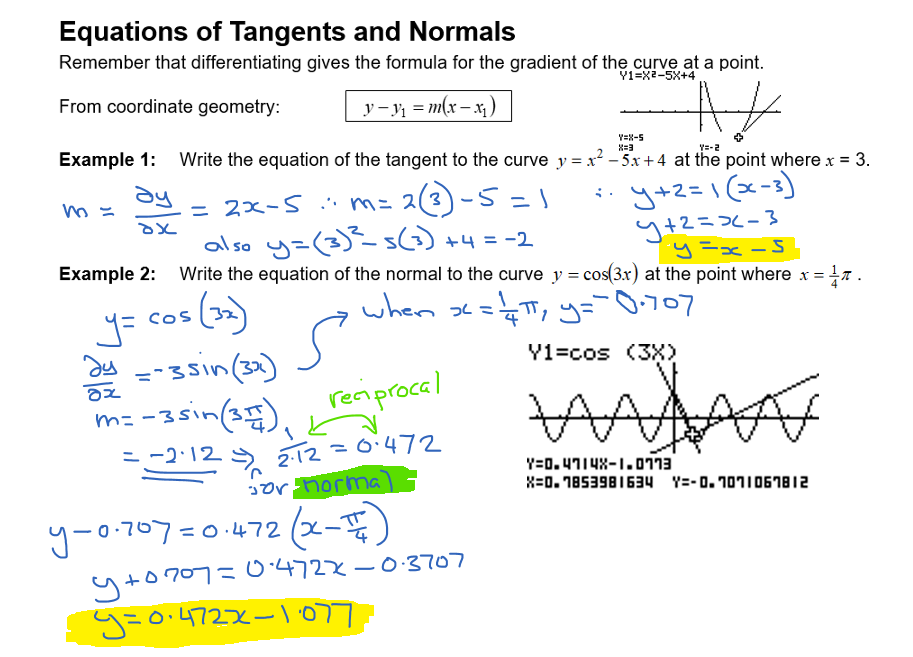
Equations Of Tangents And Normals Mathtec Show step by step solutions. core 1 differentiation 4. tangents and normals (finding equations tangent) as as & a level maths calculus. finding the gradient to a point on a curve. tangent and normal to a curve. show step by step solutions. try the free mathway calculator and problem solver below to practice various math topics. Next: fm exact trig values questions. the corbettmaths practice questions on equation of a normal for level 2 further maths. Know how to calculate the angle between tangents and normals: use the formula tan (θ) =. (m1 m2) (1 m1*m2) where m1 and m2 are the slopes of the two lines. practice finding the equation of the tangent and normal at a given point using differentiation: this will involve finding the derivative of the curve’s equation, substituting in the. Step 2: substitute the x value of the given point into the first derivative to find the gradient of the tangent. step 3: use the gradient point form of a line equation (y y1 = m(x x1)) where m is the gradient and (x1, y1) is the given point, to determine the equation of the tangent. deriving the equation of a normal. step 1: find the.

Differentiating And Equations Of Tangents Gcse Further Maths Revision Know how to calculate the angle between tangents and normals: use the formula tan (θ) =. (m1 m2) (1 m1*m2) where m1 and m2 are the slopes of the two lines. practice finding the equation of the tangent and normal at a given point using differentiation: this will involve finding the derivative of the curve’s equation, substituting in the. Step 2: substitute the x value of the given point into the first derivative to find the gradient of the tangent. step 3: use the gradient point form of a line equation (y y1 = m(x x1)) where m is the gradient and (x1, y1) is the given point, to determine the equation of the tangent. deriving the equation of a normal. step 1: find the. To find the equation of the normal line, we use the point slope form of the equation of a line, replacing the slope with the negative reciprocal of the slope of the tangent line. by understanding these key principles, you will be able to determine the equations for tangents and normals for a given function in any cartesian system. So if the gradient of the tangent at the point (2, 8) of the curve y = x 3 is 12, the gradient of the normal is 1 12, since 1 12 × 12 = 1 . the equation of the normal at the point (2, 8) is therefore: y 8 = 1 12 (x 2) hence the equation of the normal at (2,8) is 12y x = 98 . tangents and normals a level maths revision section looking.