Finding Missing Side Using Trig Ratio Math Trigonometry

Geometry 8 3b Applying Trigonometric Ratios Find The Missing Side Finding the two missing sides. to find the two unknown sides, you can use the angle α \alpha α and the trigonometric ratios: given a: c = a sin ⁡ α c = a {\sin{\alpha}} c = a sin α and b = a tan ⁡ α b = a {\tan{\alpha}} b = a tan α; given b: c = b cos ⁡ α c = b {\cos{\alpha}} c = b cos α and a = b × tan ⁡ α a = b. Trigonometry calculator as a tool for solving right triangle. to find the missing sides or angles of the right triangle, all you need to do is enter the known variables into the trigonometry calculator. you need only two given values in the case of: one side and one angle. two sides. area and one side. remember that if you know two angles, it's.

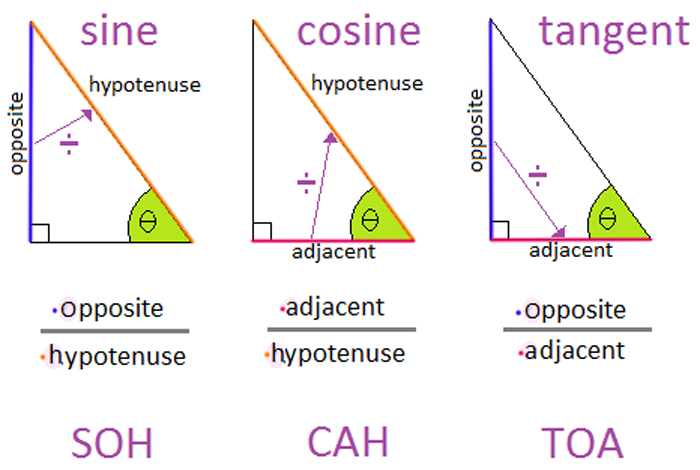
Solving For Missing Sides Using Trig Ratios Mrs Mayer S Math Class Instructions. draw the following right triangles (described below). find the missing angle for each triangle. for each triangle, use the given acute angle & side length to create a trig ratio (sine, cosine, or tangent) to solve for a missing side of your choice. each trig ratio must be used once during your lesson. Here θ = θ˚. the sides opposite and hypotenuse are involving in the trigonometric ratio sin θ. sin θ = opposite side hypotenuse side = ab ac. sin θ˚ = 4 6. sin θ˚ = 2 3. θ˚ = sin 1(2 3) by using the calculator, we get. θ = 42˚. so, the value of θ is 42˚. Math worksheets. examples, videos, worksheets, solutions, and activities to help students learn how to find the missing side of a right triangle given an angle and side using trigonometry. trigonometry: finding side length using primary trig ratios trigonometry: finding side length using primary trig ratios part 2. show step by step solutions. Right triangle trigonometry. the word trigonometry can be broken into the parts tri, gon, and metry, which means “three angle measurement,” or equivalently “triangle measurement.”. throughout this unit, we will learn new ways of finding missing sides and angles of triangles which we would be unable to find using the pythagorean theorem.

Using Trig Ratios To Find Missing Sides Trig Day 2 Youtube Math worksheets. examples, videos, worksheets, solutions, and activities to help students learn how to find the missing side of a right triangle given an angle and side using trigonometry. trigonometry: finding side length using primary trig ratios trigonometry: finding side length using primary trig ratios part 2. show step by step solutions. Right triangle trigonometry. the word trigonometry can be broken into the parts tri, gon, and metry, which means “three angle measurement,” or equivalently “triangle measurement.”. throughout this unit, we will learn new ways of finding missing sides and angles of triangles which we would be unable to find using the pythagorean theorem. Using a calculator to compute trigonometric ratios. 1. introduction: find the following trigonometric ratios by using the definitions of sin(x), cos(x), and tan(x) using the mnemonic soh cah toa and then use your calculator to change each fraction to a decimal. (round your answers to the nearest ten thousandth, i.e. four decimal places.). Trigonometric ratios: ratios that relate the lengths of the sides of right triangles to their interior angles. sine: the sine (sin) of an angle is equal to the length of the opposite (opp) side divided by the length of the hypotenuse (hypot). sin θ = opp hypot. cosine: the cosine (cos) of an angle is equal to the length of the adjacent (adj.

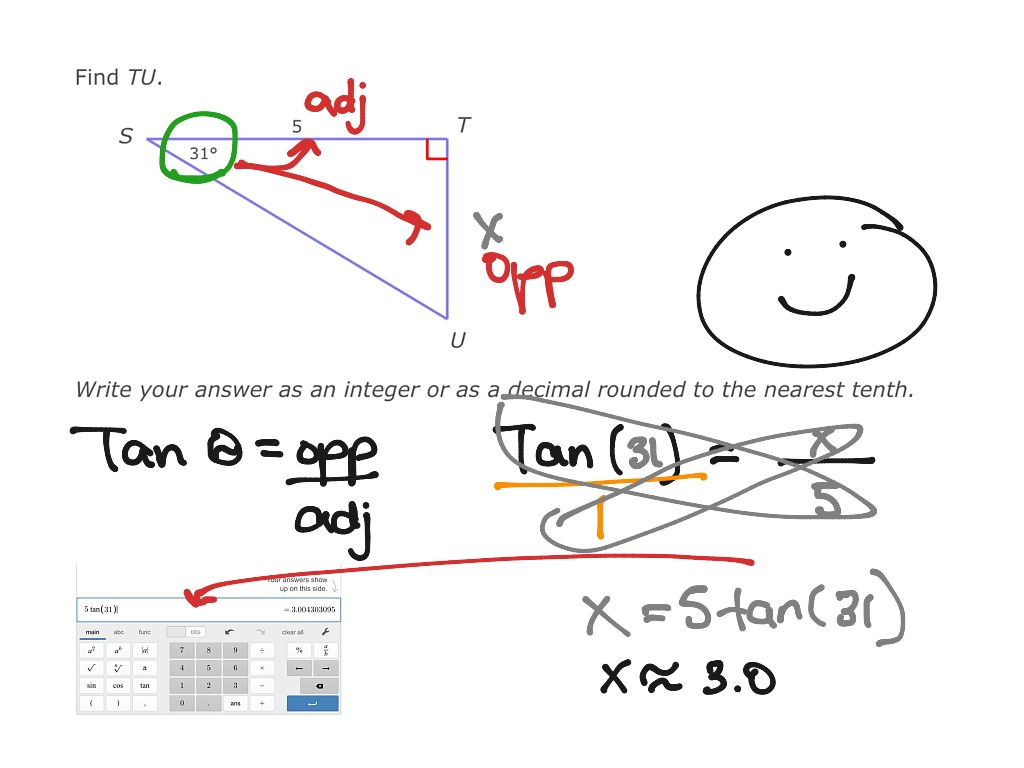
Finding Missing Side Using Trig Ratio Math Trigonometry Using a calculator to compute trigonometric ratios. 1. introduction: find the following trigonometric ratios by using the definitions of sin(x), cos(x), and tan(x) using the mnemonic soh cah toa and then use your calculator to change each fraction to a decimal. (round your answers to the nearest ten thousandth, i.e. four decimal places.). Trigonometric ratios: ratios that relate the lengths of the sides of right triangles to their interior angles. sine: the sine (sin) of an angle is equal to the length of the opposite (opp) side divided by the length of the hypotenuse (hypot). sin θ = opp hypot. cosine: the cosine (cos) of an angle is equal to the length of the adjacent (adj.