Find The Relation Between Radii Of Three Circles With Their Collinear

Find The Relation Between Radii Of Three Circles With Their Collinear In this video clip, we will discuss the relation between the radii of three touching circles whose centers lie in a straight line and there is a direct commo. Show they are always collinear for any three non intersecting circles of distinct radii. solution: we augment any such layout of three circles with a three dimensional construction: atop each circle place a cone with height equal to its radius. for any two circles, there is a line containing the apexes of their corresponding cones.

Relation Between The Radii Of Circles Rajnikant Mishra Medium Let there be three circles of different radii lying completely outside each other. to exclude a trivial case, assume also that their centers are not collinear, i.e. the three centers do not lie on the same straight line. under these conditions, six external tangents to two of the three circles, taken pairwise, intersect at three points. Given centres and the radii of three circles a, b, and c in the form of {x, y, r}, where (x, y) is the centre of the circle and r is the radius of that circle. the task is to check if any two circles intersect such that the third circle passes through the intersecting points and the centres of the two circles. if found to be true, then print "yes". Two circles are said to touch each other if they have only one point common – a common tangent can then be drawn to both the circles at that point. consider the following figure, where two circles s 1 and s 2 (with radii r 1 and r 2) touch each other externally at p. in this case, the distance between o 1 and o 2 (their centers) is r 1 r 2. Method 1: distance formula. one of the ways to prove that three points are collinear is by using the distance formula. the distance formula can calculate the distance between two points in a cartesian plane. if the sum of the two shorter distances is equal to the longest distance, then the three points are collinear.
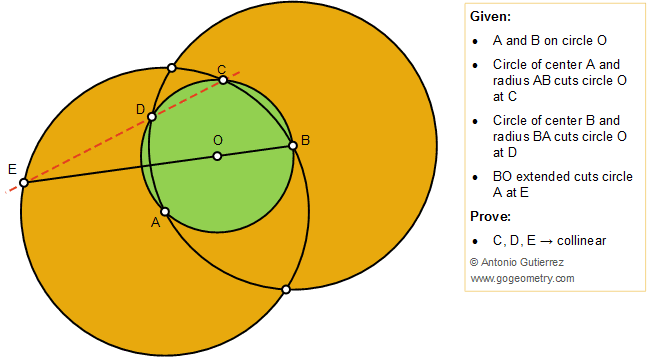
Geometry Problem 1404 Three Circles Center Intersecting Points Two circles are said to touch each other if they have only one point common – a common tangent can then be drawn to both the circles at that point. consider the following figure, where two circles s 1 and s 2 (with radii r 1 and r 2) touch each other externally at p. in this case, the distance between o 1 and o 2 (their centers) is r 1 r 2. Method 1: distance formula. one of the ways to prove that three points are collinear is by using the distance formula. the distance formula can calculate the distance between two points in a cartesian plane. if the sum of the two shorter distances is equal to the longest distance, then the three points are collinear. If you want to show that three points are collinear, choose two line segments, for example \ (ab\) and \ (bc\). you then need to establish that they have: a common direction (that is, equal. From this, the centre and radius of each circle is (5, 6) and a radius of 5 ( 4, 6) and a radius of 10. in order to prove that the circles touch externally the distance between the 2 centres is the same of the sum of the 2 radii or 15. using the distance formula i get ${{\sqrt {( 4 5)^2 ( 6 6)^2}}}$ which is ${\sqrt {81 36} = \sqrt 225.
Relation Between Radii And Angles Now Consider 3 Circles C I Where I If you want to show that three points are collinear, choose two line segments, for example \ (ab\) and \ (bc\). you then need to establish that they have: a common direction (that is, equal. From this, the centre and radius of each circle is (5, 6) and a radius of 5 ( 4, 6) and a radius of 10. in order to prove that the circles touch externally the distance between the 2 centres is the same of the sum of the 2 radii or 15. using the distance formula i get ${{\sqrt {( 4 5)^2 ( 6 6)^2}}}$ which is ${\sqrt {81 36} = \sqrt 225.

Solved Three Circles With Radii 0 Chegg

Three Circles Touch One Another Externally Their Centres Form A

Comments are closed.