Find Derivatives Of Functions In Calculus

Calculus Derivative Rules Video Lessons Examples Solutions The derivative calculator is an invaluable online tool designed to compute derivatives efficiently, aiding students, educators, and professionals alike. here's how to utilize its capabilities: begin by entering your mathematical function into the above input field, or scanning it with your camera. click the 'go' button to instantly generate the. Differential calculus 6 units · 117 skills. unit 1 limits and continuity. unit 2 derivatives: definition and basic rules. unit 3 derivatives: chain rule and other advanced topics. unit 4 applications of derivatives. unit 5 analyzing functions. unit 6 parametric equations, polar coordinates, and vector valued functions. course challenge.
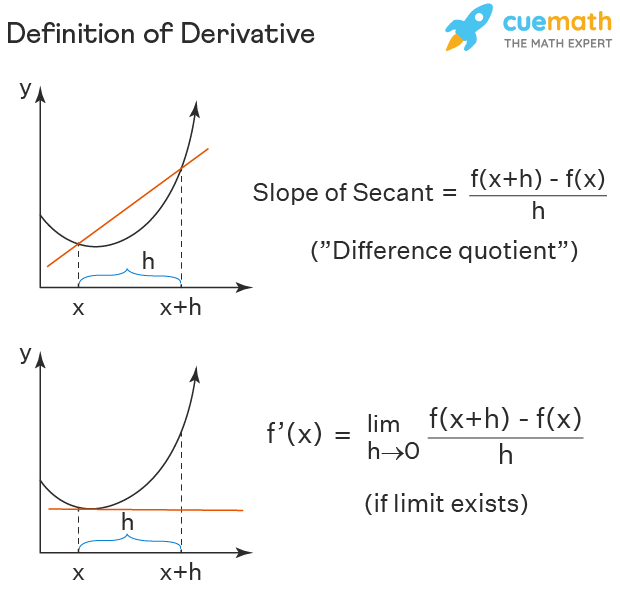
Derivatives Calculus Meaning Interpretation It means that, for the function x 2, the slope or "rate of change" at any point is 2x. so when x=2 the slope is 2x = 4, as shown here: or when x=5 the slope is 2x = 10, and so on. note: f’ (x) can also be used to mean "the derivative of": f’ (x) = 2x. "the derivative of f (x) equals 2x". or simply "f dash of x equals 2x". Definition. let f be a function. the derivative function, denoted by f ′, is the function whose domain consists of those values of x such that the following limit exists: f ′ (x) = lim h → 0f(x h) − f(x) h. (3.9) a function f(x) is said to be differentiable at a if f ′ (a) exists. Derivatives of all six trig functions are given and we show the derivation of the derivative of sin(x) sin. . (x) and tan(x) tan (x). derivatives of exponential and logarithm functions – in this section we derive the formulas for the derivatives of the exponential and logarithm functions. derivatives of inverse trig functions – in this. The derivative tells us the slope of a function at any point. there are rules we can follow to find many derivatives. for example: the slope of a constant value (like 3) is always 0; the slope of a line like 2x is 2, or 3x is 3 etc; and so on. here are useful rules to help you work out the derivatives of many functions (with examples below).

Calculus Derivative Rules Formulas Examples Solutions Videos Derivatives of all six trig functions are given and we show the derivation of the derivative of sin(x) sin. . (x) and tan(x) tan (x). derivatives of exponential and logarithm functions – in this section we derive the formulas for the derivatives of the exponential and logarithm functions. derivatives of inverse trig functions – in this. The derivative tells us the slope of a function at any point. there are rules we can follow to find many derivatives. for example: the slope of a constant value (like 3) is always 0; the slope of a line like 2x is 2, or 3x is 3 etc; and so on. here are useful rules to help you work out the derivatives of many functions (with examples below). 3.3.3 use the product rule for finding the derivative of a product of functions. 3.3.4 use the quotient rule for finding the derivative of a quotient of functions. 3.3.5 extend the power rule to functions with negative exponents. 3.3.6 combine the differentiation rules to find the derivative of a polynomial or rational function. If a function is differentiable at a point, then it is continuous at that point. 3.2e: exercises for section 3.2; 3.3: differentiation rules the derivative of a constant function is zero. the derivative of a power function is a function in which the power on x becomes the coefficient of the term and the power on x in the derivative decreases by 1.

Comments are closed.