Find Angles In Polygons Within Regular Polygons

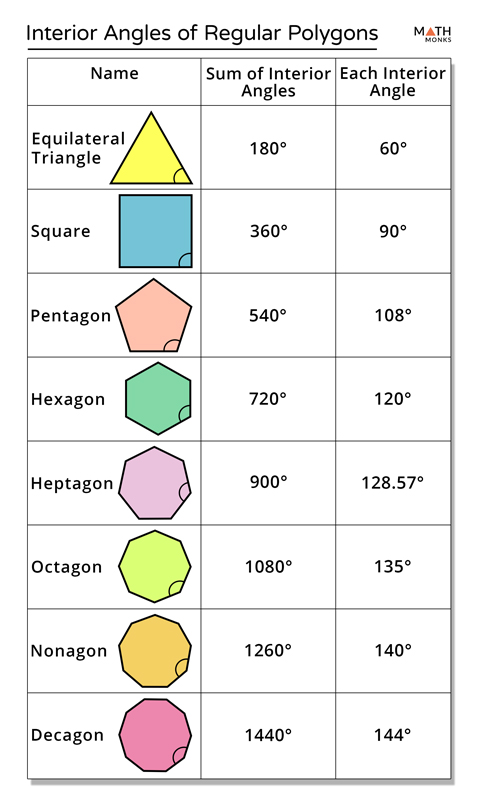
Find Angle Measures In Polygons Octagon. octagons have 8 sides so again, we need to adjust the formula accordingly: sum of internal angles = (8 2) x 180°. 1080° = 6 x 180°. in a regular octagon, one angle would be worth. If it is a regular polygon (all sides are equal, all angles are equal) shape sides sum of interior angles shape each angle; triangle: 3: 180° 60° quadrilateral: 4: 360° 90° pentagon: 5: 540° 108° hexagon: 6: 720° 120° heptagon (or septagon) 7: 900° 128.57 ° octagon: 8: 1080° 135° nonagon: 9: 1260° 140° any polygon: n (n−2.

Interior Angles Of Regular Polygons A Plus Topper The polygon can be broken up into three triangles. multiply the number of triangles by 180o to get the sum of the interior angles. show step. 180∘ ×3 = 540∘ 180 ∘ × 3 = 540 ∘. state your findings e.g. sides, regular irregular, the sum of interior angles. show step. The angles of a regular polygon can easily be found using the methods of section 1.5. figure \(\pageindex{1}\): examples of regular polygons. suppose we draw the angle bisector of each angle of a regular polygon, we will find these angle bisectors all meet at the same point (figure \(\pageindex{2}\)). Misidentifying if a polygon is regular or irregular make it clear that regular polygons have equal interior and exterior angles, but irregular polygons do not. teach students to recognize when a polygon is regular versus irregular and to adjust their calculations as needed. forgetting that interior and exterior angles are supplementary. Scroll down the page for more examples and solutions on the interior angles of a polygon. example: find the sum of the interior angles of a heptagon (7 sided) solution: step 1: write down the formula (n 2) × 180°. step 2: plug in the values to get (7 2) × 180° = 5 × 180° = 900°. answer: the sum of the interior angles of a heptagon (7.
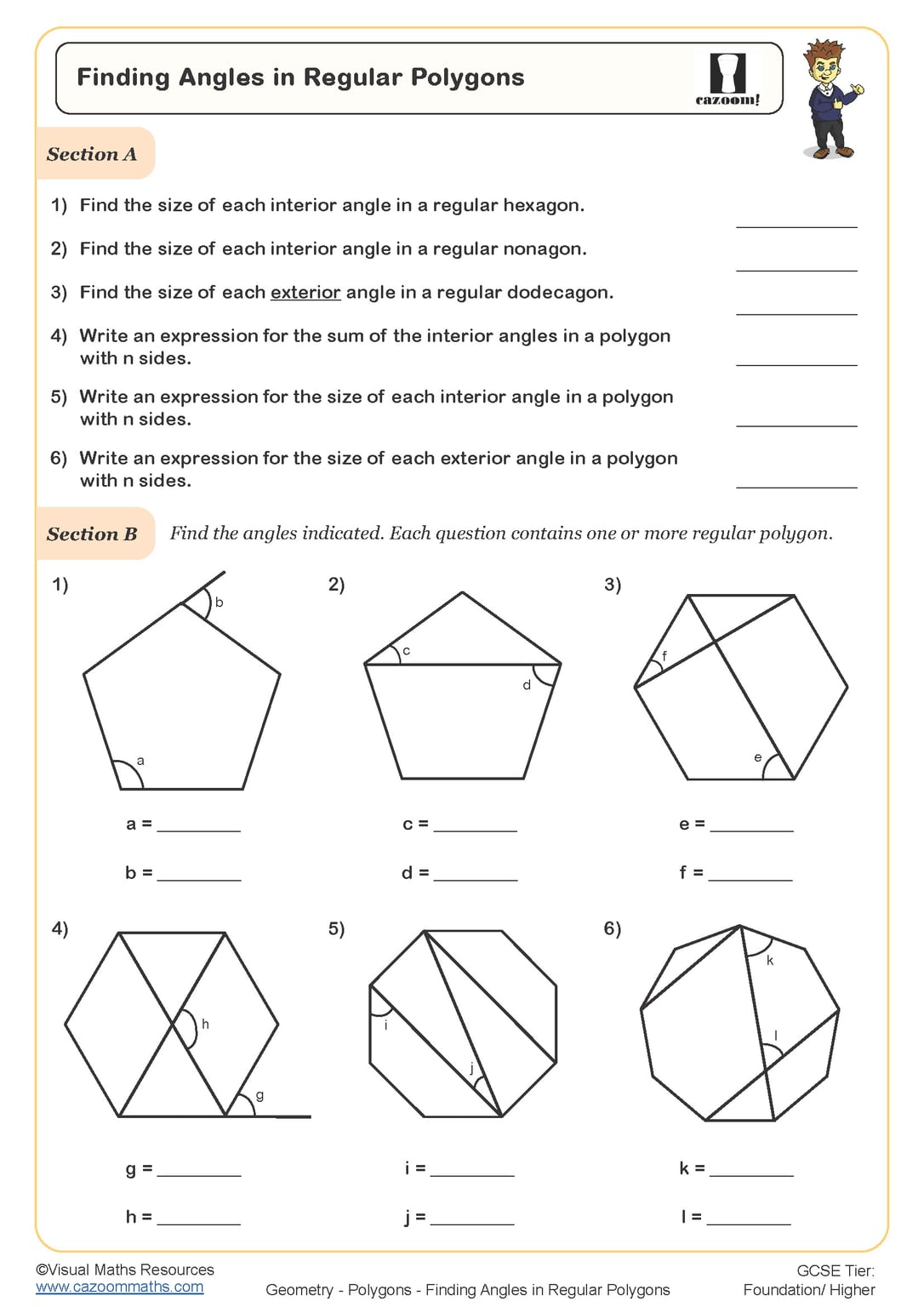
Finding Angles In Regular Polygons Worksheet Cazoom Maths Worksheets Misidentifying if a polygon is regular or irregular make it clear that regular polygons have equal interior and exterior angles, but irregular polygons do not. teach students to recognize when a polygon is regular versus irregular and to adjust their calculations as needed. forgetting that interior and exterior angles are supplementary. Scroll down the page for more examples and solutions on the interior angles of a polygon. example: find the sum of the interior angles of a heptagon (7 sided) solution: step 1: write down the formula (n 2) × 180°. step 2: plug in the values to get (7 2) × 180° = 5 × 180° = 900°. answer: the sum of the interior angles of a heptagon (7. To find the sum of interior angles of a polygon, multiply the number of triangles in the polygon by 180°. the formula for calculating the sum of interior angles is \ ( (n 2) \times 180^\circ. Determine the size of the angles and or side lengths within the polygon. show step. as the angle at o o for each isosceles triangle is equal to 45° 45°, the other two angles must be equal to (180 45) ÷ 2 = 67.5°. (180 − 45) ÷ 2 = 67.5°. two adjacent angles are therefore equal to 67.5 × 2 = 135°. 67.5 × 2 = 135°.

Angles In A Regular Polygon Maths Tutor Bournemouth To find the sum of interior angles of a polygon, multiply the number of triangles in the polygon by 180°. the formula for calculating the sum of interior angles is \ ( (n 2) \times 180^\circ. Determine the size of the angles and or side lengths within the polygon. show step. as the angle at o o for each isosceles triangle is equal to 45° 45°, the other two angles must be equal to (180 45) ÷ 2 = 67.5°. (180 − 45) ÷ 2 = 67.5°. two adjacent angles are therefore equal to 67.5 × 2 = 135°. 67.5 × 2 = 135°.
Regular And Irregular Polygons Definition Differences

Comments are closed.