Figure 2 1 From Applications Of 3 Manifold Floer Homology By Ilya Elson

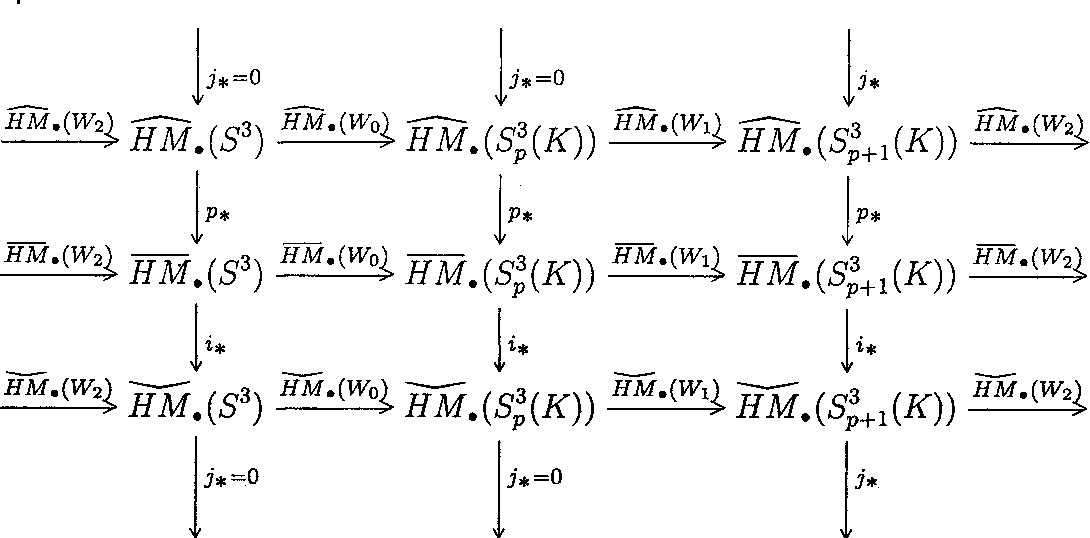
Figure 2 1 From Applications Of 3 Manifold Floer Homology By Ilya Elson Is a cobordism from m2 to m4, then w1 x m2 ihmxm3 2 m3 x w2 is a cobordism from m1 x m2 to m3 x m4.the cobordism ring q is known to be generated by cp', n > 2. a refinement of the notion of cobordism is the notion of oriented cobordism. namely, an oriented cobordism between oriented manifolds m1 and m2, is an ori ented manifold w, such that aw. In this thesis we give an exposition of some of the topological preliminaries necessary to understand 3 manifold floer homology constructed by peter kronheimer and tomasz mrowka in [16], along with some properties of this theory, calculations for specific manifolds, and applications to 3 manifold topology.

Applications Of 3 Manifold Floer Homology Abstract. in this thesis we give an exposition of some of the topological preliminaries necessary to understand 3 manifold floer homology constructed by peter kronheimer and tomasz mrowka in [16], along with some properties of this theory, calculations for specific manifolds, and applications to 3 manifold topology. Preface 1. surface bundles 2. the topology of s1 3. minimal surfaces 4. taut foliations 5. finite depth foliations 6. essential laminations 7. universal circles 8. constructing transverse laminations … expand. Download citation | applications of 3 manifold floer homology | thesis (s.m.) massachusetts institute of technology, dept. of mathematics, 2007. includes bibliographical references (leaves 34 47). With ∂n =s2 is equivalent to give a closed 3 manifold. so in the case when Σ=s2 the axiom (1.6) should give the description of floer homology of connected sum of two closed 3 manifolds. such a description is given in [20], [30]. from them, it is obvious that we need more information to describe floer homology of n1# n2 than “lagrangian.

Figure 2 From A Simplification Of Combinatorial Link Floer Homology Download citation | applications of 3 manifold floer homology | thesis (s.m.) massachusetts institute of technology, dept. of mathematics, 2007. includes bibliographical references (leaves 34 47). With ∂n =s2 is equivalent to give a closed 3 manifold. so in the case when Σ=s2 the axiom (1.6) should give the description of floer homology of connected sum of two closed 3 manifolds. such a description is given in [20], [30]. from them, it is obvious that we need more information to describe floer homology of n1# n2 than “lagrangian. Heegaard floer homology, defined by ozsvath szab´ o in the early 2000s, is a package of invariants for´ 3 and 4 dimensional manifolds, as well as for embedded knots and surfaces inside them. in its simplest form, to a closed 3 manifold y, heegaard floer homology associates a graded vector space hfd(y). a. Embedded contact homology, due to michael hutchings, is an invariant of 3 manifolds (with a distinguished second homology class, corresponding to the choice of a spin c structure in seiberg–witten floer homology) isomorphic (by work of clifford taubes) to seiberg–witten floer cohomology and consequently (by work announced by kutluhan, lee.

Figure 2 From Functors And Computations In Floer Homology With Heegaard floer homology, defined by ozsvath szab´ o in the early 2000s, is a package of invariants for´ 3 and 4 dimensional manifolds, as well as for embedded knots and surfaces inside them. in its simplest form, to a closed 3 manifold y, heegaard floer homology associates a graded vector space hfd(y). a. Embedded contact homology, due to michael hutchings, is an invariant of 3 manifolds (with a distinguished second homology class, corresponding to the choice of a spin c structure in seiberg–witten floer homology) isomorphic (by work of clifford taubes) to seiberg–witten floer cohomology and consequently (by work announced by kutluhan, lee.

Figure 2 From Functors And Computations In Floer Homology With