Fibonacci Sequence Golden Ratio Geometric Shapes Spiral Snail Spiral
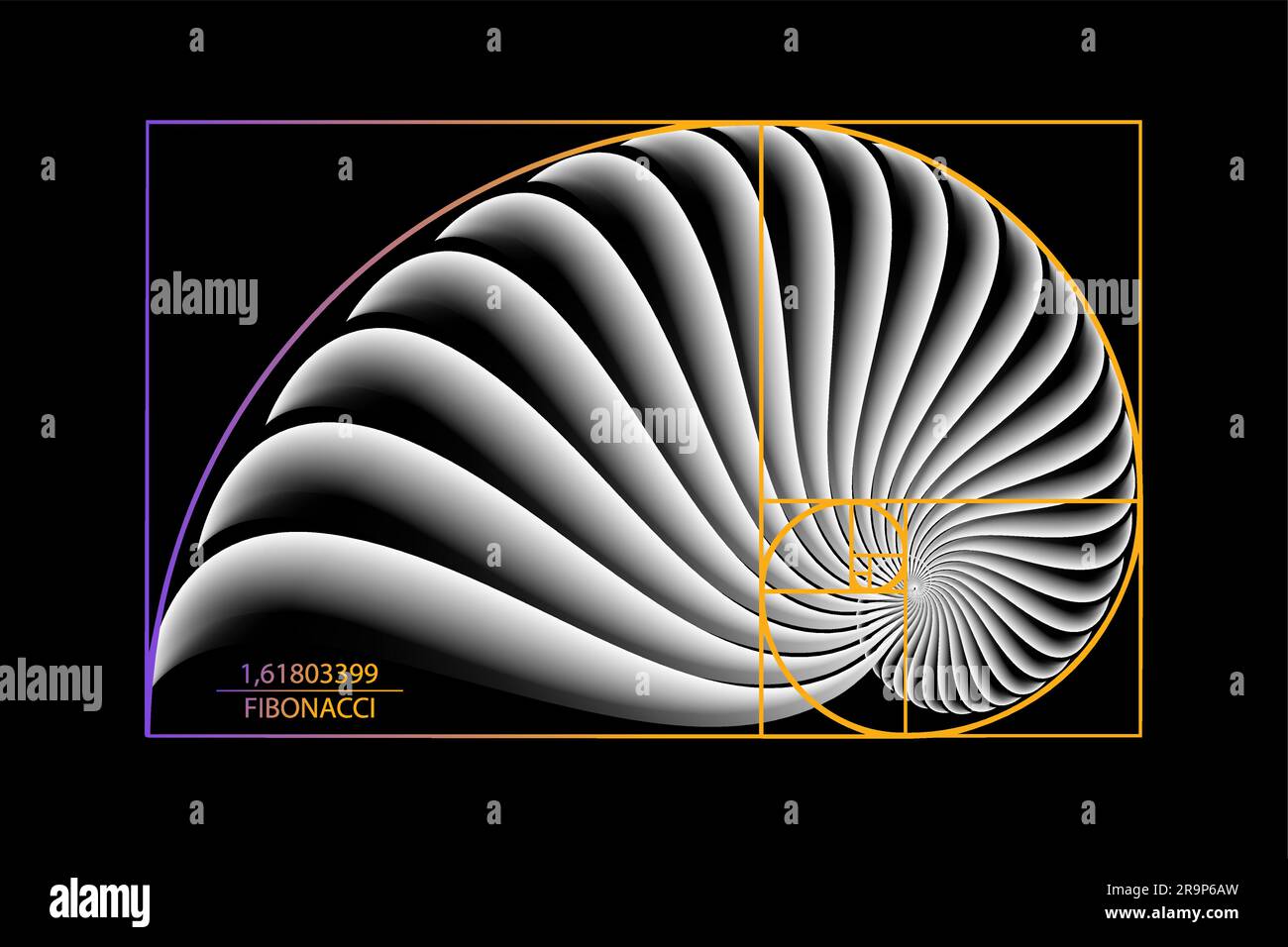
Fibonacci Sequence Golden Ratio Geometric Shapes Spiral Snail Spiral This resulting golden spiral is often associated with the nautilus spiral, but incorrectly because the two spirals are clearly very different. a golden spiral created from a golden rectangle expands in dimension by the golden ratio with every quarter, or 90 degree, turn of the spiral. this can be constructed by starting with a golden rectangle. The fibonacci spiral gets closer and closer to a golden spiral as it increases in size because of the ratio of each number in the fibonacci series to the one before it converges on phi, 1.618, as the series progresses (e.g., 1, 1, 2, 3, 5, 8 and 13 produce ratios of 1, 2, 1.5, 1.67, 1.6 and 1.625, respectively) fibonacci spirals and golden.

Fibonacci Sequence Golden Ratio Gold Geometric Shapes Spiral Colorful Mathematicians have learned to use fibonacci’s sequence to describe certain shapes that appear in nature. these shapes are called logarithmic spirals, and nautilus shells are just one example. Put simply, the fibonacci sequence is a series of numbers which begins with 1 and 1. from there, you add the previous two numbers in the sequence together, to get the next number. this is a type. Golden spiral. golden spirals are self similar. the shape is infinitely repeated when magnified. in geometry, a golden spiral is a logarithmic spiral whose growth factor is φ, the golden ratio. [1] that is, a golden spiral gets wider (or further from its origin) by a factor of φ for every quarter turn it makes. This process can be repeated to infinity to obtain in this way a series of nested rectangles, one inside the other in the form of a spiral (fig 5). this very special spiral (called the logarithmic spiral) is exactly that of the nautilus shell and of certain snails (the planorbe or flat snail).
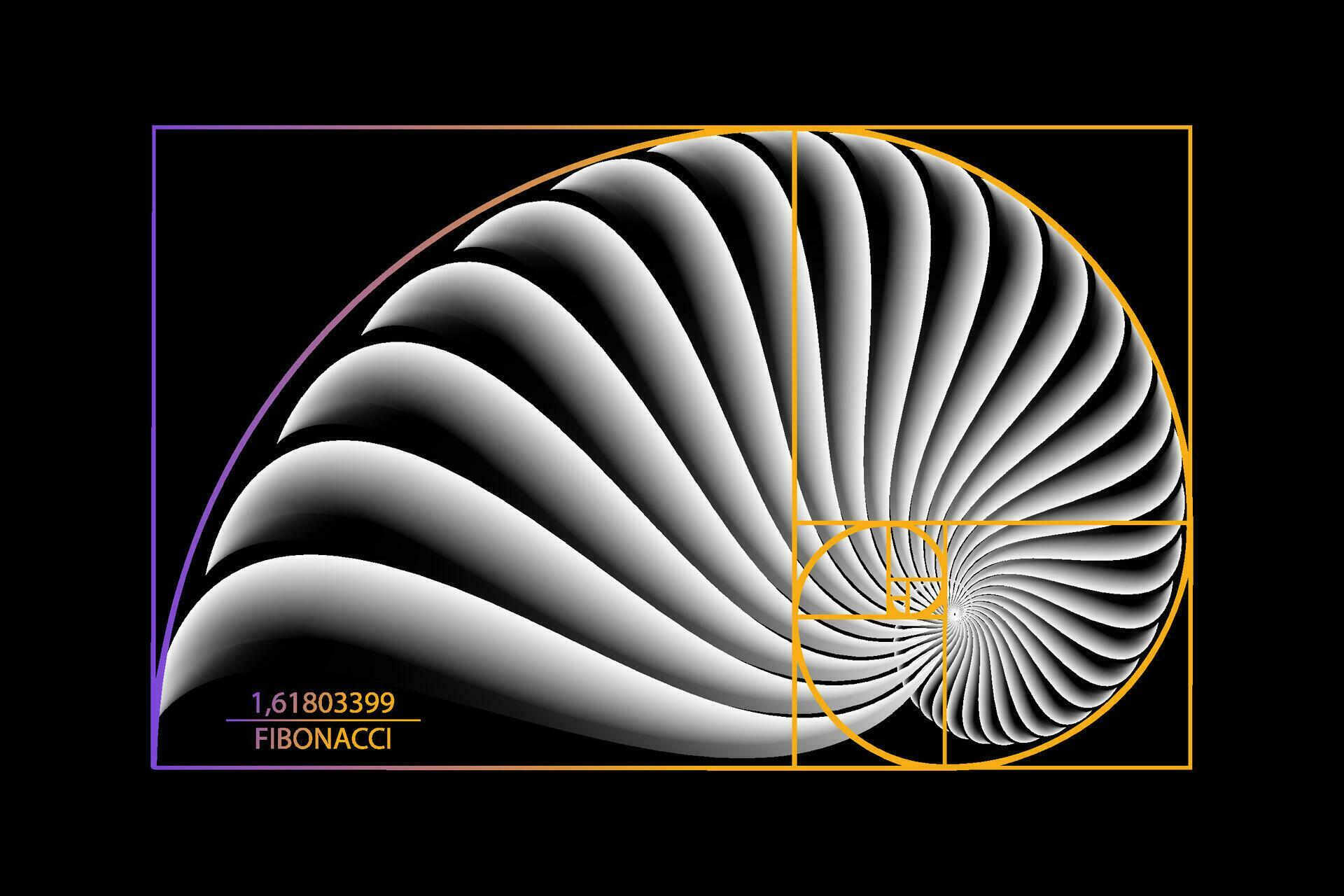
Fibonacci Sequence Golden Ratio Geometric Shapes Spiral Snail Spiral Golden spiral. golden spirals are self similar. the shape is infinitely repeated when magnified. in geometry, a golden spiral is a logarithmic spiral whose growth factor is φ, the golden ratio. [1] that is, a golden spiral gets wider (or further from its origin) by a factor of φ for every quarter turn it makes. This process can be repeated to infinity to obtain in this way a series of nested rectangles, one inside the other in the form of a spiral (fig 5). this very special spiral (called the logarithmic spiral) is exactly that of the nautilus shell and of certain snails (the planorbe or flat snail). Spirals are the most common galaxy shape. galaxies group together in superclusters and superclusters group together in walls. these walls or filaments of numerous superclusters, gravitationally bound and separated by large areas of void, are the largest known structures in the universe. The mathematical ideas the fibonacci sequence leads to, such as the golden ratio, spirals and self similar curves, have long been appreciated for their charm and beauty, but no one can really explain why they are echoed so clearly in the world of art and nature. the story began in pisa, italy in the year 1202.
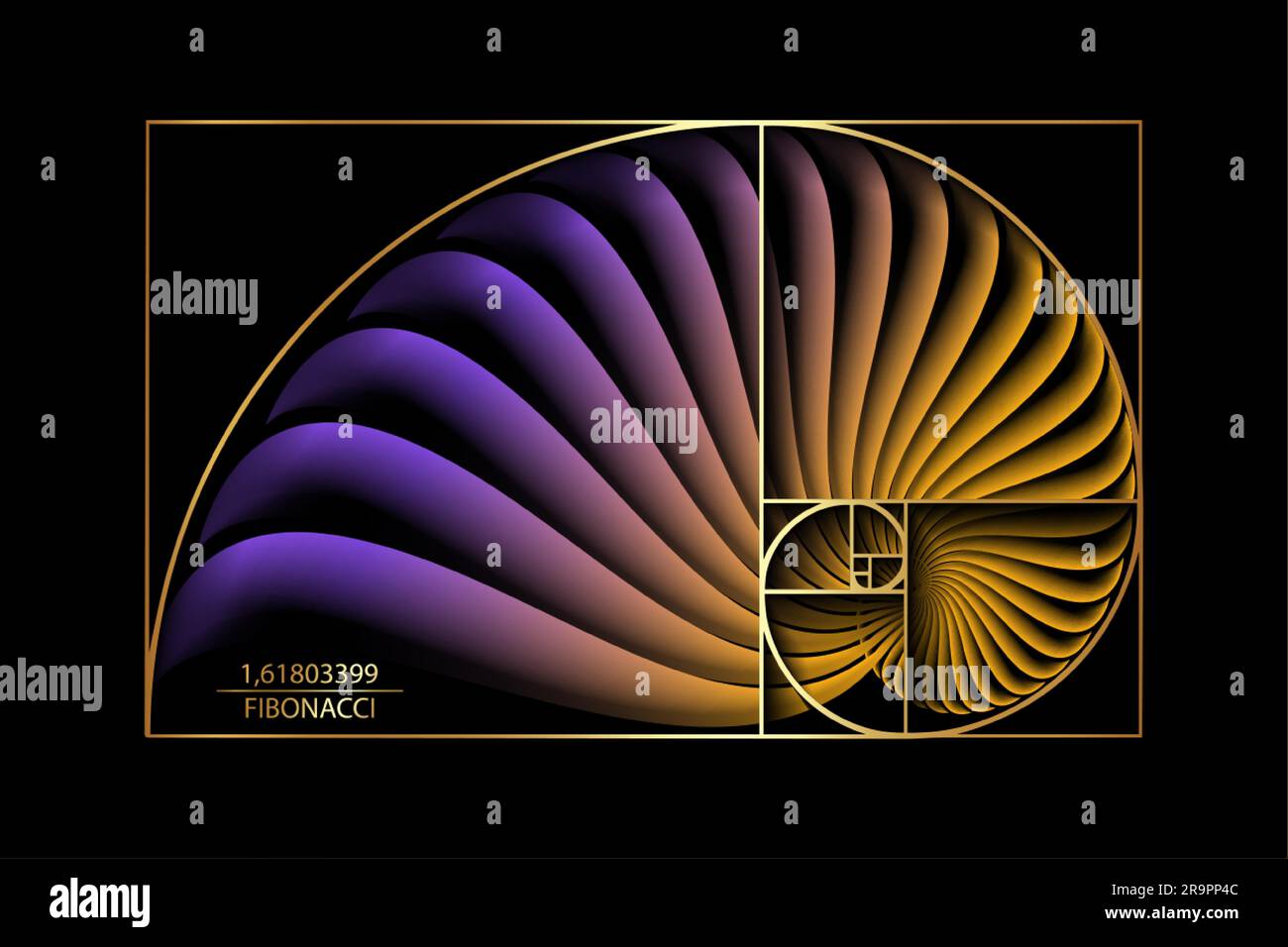
Fibonacci Sequence Golden Ratio Gold Geometric Shapes Spiral Colorful Spirals are the most common galaxy shape. galaxies group together in superclusters and superclusters group together in walls. these walls or filaments of numerous superclusters, gravitationally bound and separated by large areas of void, are the largest known structures in the universe. The mathematical ideas the fibonacci sequence leads to, such as the golden ratio, spirals and self similar curves, have long been appreciated for their charm and beauty, but no one can really explain why they are echoed so clearly in the world of art and nature. the story began in pisa, italy in the year 1202.

Comments are closed.