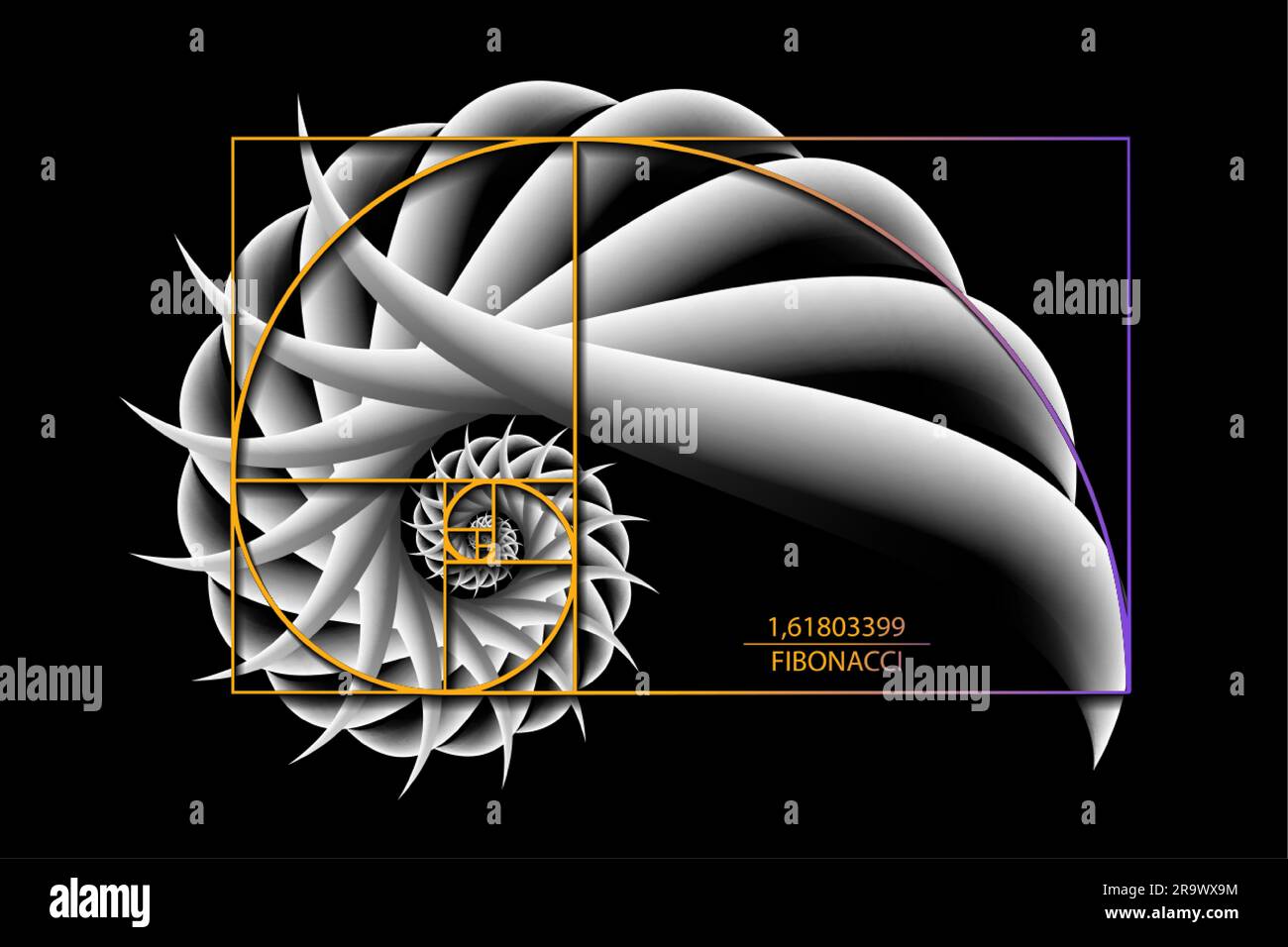
Fibonacci Sequence Golden Ratio Geometric Shapes Spiral 3d Snail A tiling with squares whose side lengths are successive fibonacci numbers via . mathematicians have learned to use fibonacci’s sequence to describe certain shapes that appear in nature. The fibonacci sequence is named after leonardo of pisa, who was known as fibonacci. though fibonacci first introduced the sequence to the western world in 1202, it had been noted by indian mathematicians as early as the sixth century .
Premium Vector Fibonacci Sequence Golden Ratio Geometric Shapes This article does not use the fibonacci sequence to draw the golden spiral. your point is valid that a fibonacci spiral approximate the golden spiral as the numbers grow. the illustrations shown however use a true golden spiral, which is based on successive golden rectangles whose sides are already in the ratio of 1.618… to 1. The fibonacci spiral gets closer and closer to a golden spiral as it increases in size because of the ratio of each number in the fibonacci series to the one before it converges on phi, 1.618, as the series progresses (e.g., 1, 1, 2, 3, 5, 8 and 13 produce ratios of 1, 2, 1.5, 1.67, 1.6 and 1.625, respectively) fibonacci spirals and golden. This process can continue forever, making a sequence of rectangles, each following the golden ratio. as the sequence goes on, we compose the famous golden spiral – an image often used to represent the golden ratio: what does the fibonacci sequence have to do with the golden ratio? the fibonacci sequence is a series of numbers that goes on. If we extend the series out indefinitely, the ratio approaches ~1.618:1, a constant we call phi, that is represented by the greek letter φ. 3 petals. 5 petals. 8 petals. 13 petals. 21 petals. video: watch the following video for a nice explanation.
Premium Vector 3d Fibonacci Sequence Golden Ratio Geometric Shapes This process can continue forever, making a sequence of rectangles, each following the golden ratio. as the sequence goes on, we compose the famous golden spiral – an image often used to represent the golden ratio: what does the fibonacci sequence have to do with the golden ratio? the fibonacci sequence is a series of numbers that goes on. If we extend the series out indefinitely, the ratio approaches ~1.618:1, a constant we call phi, that is represented by the greek letter φ. 3 petals. 5 petals. 8 petals. 13 petals. 21 petals. video: watch the following video for a nice explanation. Golden spiral. golden spirals are self similar. the shape is infinitely repeated when magnified. in geometry, a golden spiral is a logarithmic spiral whose growth factor is φ, the golden ratio. [1] that is, a golden spiral gets wider (or further from its origin) by a factor of φ for every quarter turn it makes. Mathematically, the fibonacci sequence corresponds to the formation of a spiral shape in geometric representations. this type of fibonacci based spiral evolution is widely observed in nature.
Comments are closed.