Fibonacci Sequence Definition And Formula

Fibonacci Sequence Definition Formula List Examples Diagrams Fibonacci sequence is defined as the sequence of numbers and each number is equal to the sum of two previous numbers. visit byju’s to learn fibonacci numbers, definitions, formulas and examples. Fibonacci sequence formula: fibonacci sequence, the sequence of numbers 1, 1, 2, 3, 5, 8, 13, 21, …, each of which, after the second, is the sum of the two previous numbers; that is, the nth fibonacci number fn = fn − 1 fn − 2. in the fibonacci sequence, each number in the series is calculated by adding the two numbers before it.

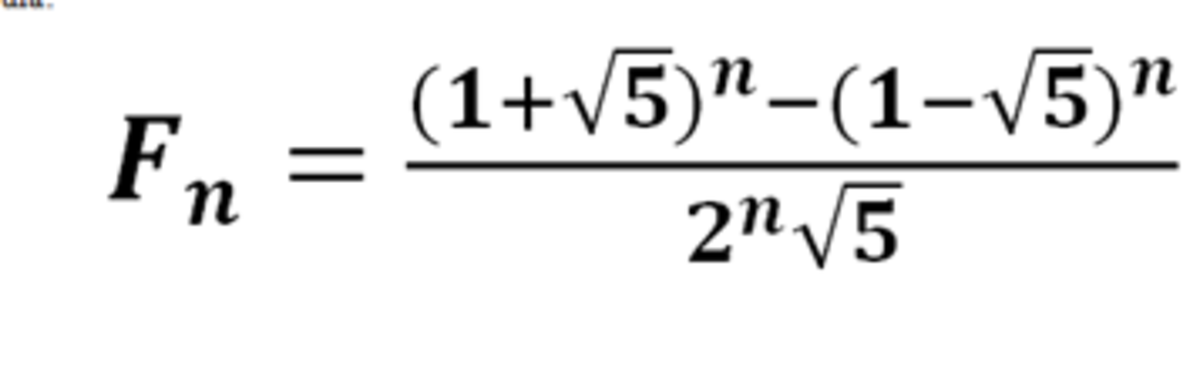
Fibonacci Sequence Formula Explained Images Solved examples. find the sum of the first 15 fibonacci numbers. solution: as we know, the sum of the fibonacci sequence = ∑ i = 0 n f i = f n 2 – f 2. = f n 2 − 1, where f n is the nth fibonacci number, and the sequence starts from f 0. thus, the sum of the first 15 fibonacci numbers = (15 2) th term – 2 nd term. The fibonacci sequence has several interesting properties. 1) fibonacci numbers are related to the golden ratio. any fibonacci number can be calculated (approximately) using the golden ratio, f n = (Φ n (1 Φ) n) √5 (which is commonly known as "binet formula"), here φ is the golden ratio and Φ ≈ 1.618034. Fibonacci sequence, the sequence of numbers 1, 1, 2, 3, 5, 8, 13, 21, …, each of which, after the second, is the sum of the two previous numbers. the numbers of the sequence occur throughout nature, and the ratios between successive terms of the sequence tend to the golden ratio. Fibonacci sequence. in mathematics, the fibonacci sequence is a sequence in which each number is the sum of the two preceding ones. numbers that are part of the fibonacci sequence are known as fibonacci numbers, commonly denoted fn . many writers begin the sequence with 0 and 1, although some authors start it from 1 and 1 [1][2] and some (as.

The Fibonacci Sequence Explained Fibonacci sequence, the sequence of numbers 1, 1, 2, 3, 5, 8, 13, 21, …, each of which, after the second, is the sum of the two previous numbers. the numbers of the sequence occur throughout nature, and the ratios between successive terms of the sequence tend to the golden ratio. Fibonacci sequence. in mathematics, the fibonacci sequence is a sequence in which each number is the sum of the two preceding ones. numbers that are part of the fibonacci sequence are known as fibonacci numbers, commonly denoted fn . many writers begin the sequence with 0 and 1, although some authors start it from 1 and 1 [1][2] and some (as. Here is a short list of the fibonacci sequence: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 as already stated, each number in the sequence is the sum of the two numbers before it. we can try to derive a fibonacci sequence formula by making some observations. Fibonacci was not the first to know about the sequence, it was known in india hundreds of years before! about fibonacci the man. his real name was leonardo pisano bogollo, and he lived between 1170 and 1250 in italy. "fibonacci" was his nickname, which roughly means "son of bonacci".

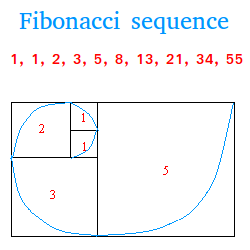
Fibonacci Sequence Definition And Formula Here is a short list of the fibonacci sequence: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 as already stated, each number in the sequence is the sum of the two numbers before it. we can try to derive a fibonacci sequence formula by making some observations. Fibonacci was not the first to know about the sequence, it was known in india hundreds of years before! about fibonacci the man. his real name was leonardo pisano bogollo, and he lived between 1170 and 1250 in italy. "fibonacci" was his nickname, which roughly means "son of bonacci".