Fibonacci Sequence Circle Golden Ratio Geometric Shapes Spiral Snail

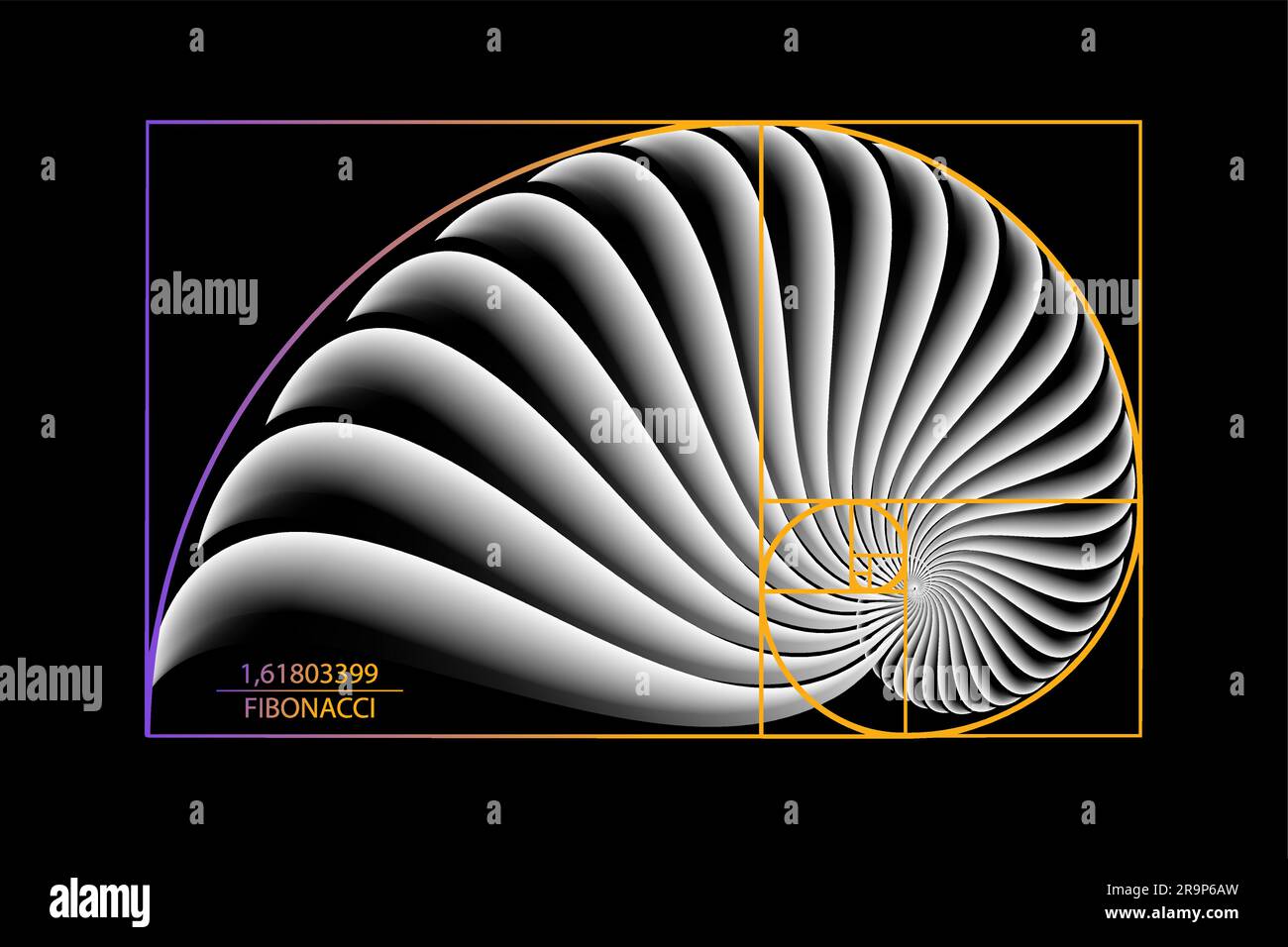
Fibonacci Sequence Golden Ratio Geometric Shapes Spiral Snail Spiral A tiling with squares whose side lengths are successive fibonacci numbers via . mathematicians have learned to use fibonacci’s sequence to describe certain shapes that appear in nature. This resulting golden spiral is often associated with the nautilus spiral, but incorrectly because the two spirals are clearly very different. a golden spiral created from a golden rectangle expands in dimension by the golden ratio with every quarter, or 90 degree, turn of the spiral. this can be constructed by starting with a golden rectangle.

Fibonacci Sequence Circle Golden Ratio Geometric Shapes Spiral Snail The fibonacci sequence is named after leonardo of pisa, who was known as fibonacci. though fibonacci first introduced the sequence to the western world in 1202, it had been noted by indian mathematicians as early as the sixth century . A golden spiral is very similar to the fibonacci spiral but is based on a series of identically proportioned golden rectangles, each having a golden ratio of 1.618 of the length of the long side to that of the short side of the rectangle: the fibonacci spiral gets closer and closer to a golden spiral as it increases in size because of the ratio. From honeybee families to flower petals, let's take a closer look at some fascinating examples of the golden ratio in flora and fauna. 1. honeybees. believe it or not, but the honeybee’s family tree, specifically how they inherit their dna, closely follows the fibonacci sequence and the golden ratio. Golden spiral. golden spirals are self similar. the shape is infinitely repeated when magnified. in geometry, a golden spiral is a logarithmic spiral whose growth factor is φ, the golden ratio. [1] that is, a golden spiral gets wider (or further from its origin) by a factor of φ for every quarter turn it makes.

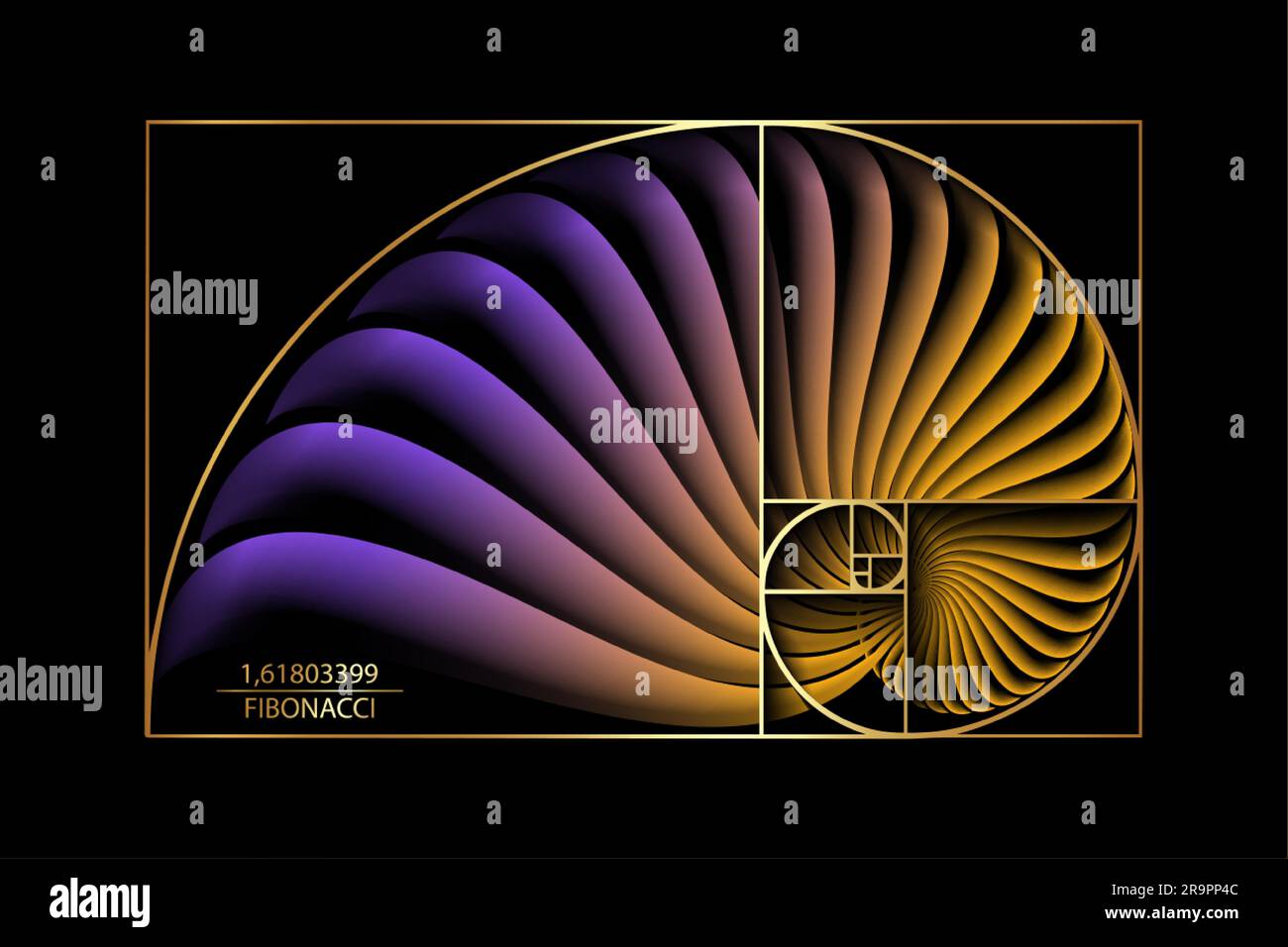
Fibonacci Sequence Golden Ratio Gold Geometric Shapes Spiral Colorful From honeybee families to flower petals, let's take a closer look at some fascinating examples of the golden ratio in flora and fauna. 1. honeybees. believe it or not, but the honeybee’s family tree, specifically how they inherit their dna, closely follows the fibonacci sequence and the golden ratio. Golden spiral. golden spirals are self similar. the shape is infinitely repeated when magnified. in geometry, a golden spiral is a logarithmic spiral whose growth factor is φ, the golden ratio. [1] that is, a golden spiral gets wider (or further from its origin) by a factor of φ for every quarter turn it makes. If we extend the series out indefinitely, the ratio approaches ~1.618:1, a constant we call phi, that is represented by the greek letter φ. 3 petals. 5 petals. 8 petals. 13 petals. 21 petals. video: watch the following video for a nice explanation. The mathematical ideas the fibonacci sequence leads to, such as the golden ratio, spirals and self similar curves, have long been appreciated for their charm and beauty, but no one can really explain why they are echoed so clearly in the world of art and nature. the story began in pisa, italy in the year 1202.