Fibonacci Sequence And Binet S Formula Hubpages

Fibonacci Sequence And Binet S Formula Hubpages Binet's formula. binet's formula is an explicit formula used to find the nth term of the fibonacci sequence. it is so named because it was derived by mathematician jacques philippe marie binet, though it was already known by abraham de moivre. we can also use the derived formula below. this is the general form for the nth fibonacci number. Binet's formula is an explicit formula used to find the th term of the fibonacci sequence. it is so named because it was derived by mathematician jacques philippe marie binet, though it was already known by abraham de moivre.

Fibonacci Sequence And Binet S Formula Hubpages Portrait of leonardo fibonacci (c.1170 c.1250), an italian mathematician. nowadays fibonacci is best known for the number sequence named after him and for spreading arabic numerical system. the rabbit problem. in his book liber abaci from the 1202 nd leonardo of pisa (fibonacci) posed following the rabbit problem. The rule that makes the fibonacci sequence is the next number is the sum of the previous two . this kind of rule is sometimes called a currerence elation.r mathematically, this is written as: f n = f n 1 f n 2 there is an explicit formula for the n th fibonacci number known as binet's formula: f n = 1 p 5 1 p 5 2! n 1 p 5 1 p 5 2! n. Binet's formula is an explicit formula for finding the nth term of the fibonacci sequence without needing to calculate all the previous terms. it expresses the nth fibonacci number as a function of n using the golden ratio, $$\frac{(\\phi^n (1 \\phi)^n)}{\\sqrt{5}}$$, where $$\\phi = \\frac{1 \\sqrt{5}}{2}$$. this formula is significant because it provides a direct way to compute. Using generating functions à la wilf's "generatingfunctionology".define the ordinary generating function: $$ f(z) = \sum {n \ge 0} f n z^n $$ the fibonacci.
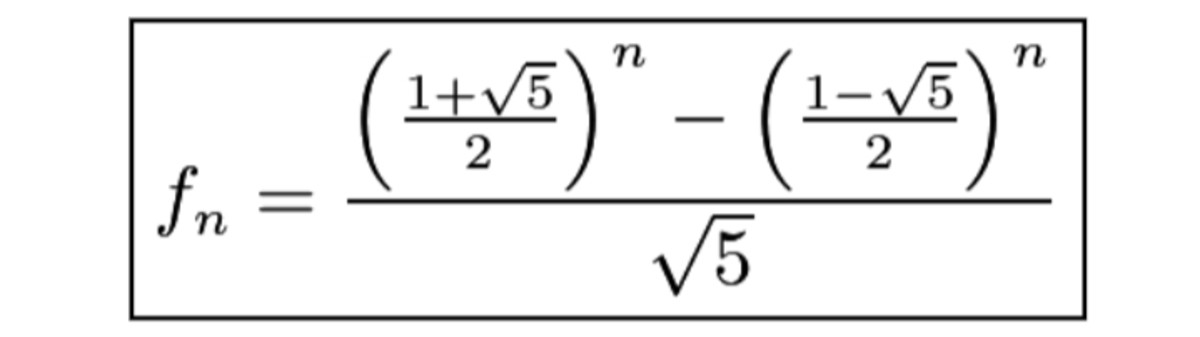
Fibonacci Sequence And Binet S Formula Hubpages Binet's formula is an explicit formula for finding the nth term of the fibonacci sequence without needing to calculate all the previous terms. it expresses the nth fibonacci number as a function of n using the golden ratio, $$\frac{(\\phi^n (1 \\phi)^n)}{\\sqrt{5}}$$, where $$\\phi = \\frac{1 \\sqrt{5}}{2}$$. this formula is significant because it provides a direct way to compute. Using generating functions à la wilf's "generatingfunctionology".define the ordinary generating function: $$ f(z) = \sum {n \ge 0} f n z^n $$ the fibonacci. The ratios , , , , , , between successive terms of the sequence tend towards the limit , a constant often denoted (the greek letter phi, also written ). is a solution of the quadratic equation . the other root is (the greek letter psi). one possible explanation for this fact is that the fibonacci numbers are given explicitly by binet's formula. Solved examples. find the sum of the first 15 fibonacci numbers. solution: as we know, the sum of the fibonacci sequence = ∑ i = 0 n f i = f n 2 – f 2. = f n 2 − 1, where f n is the nth fibonacci number, and the sequence starts from f 0. thus, the sum of the first 15 fibonacci numbers = (15 2) th term – 2 nd term.

Fibonacci Sequence And Binet S Formula Hubpages The ratios , , , , , , between successive terms of the sequence tend towards the limit , a constant often denoted (the greek letter phi, also written ). is a solution of the quadratic equation . the other root is (the greek letter psi). one possible explanation for this fact is that the fibonacci numbers are given explicitly by binet's formula. Solved examples. find the sum of the first 15 fibonacci numbers. solution: as we know, the sum of the fibonacci sequence = ∑ i = 0 n f i = f n 2 – f 2. = f n 2 − 1, where f n is the nth fibonacci number, and the sequence starts from f 0. thus, the sum of the first 15 fibonacci numbers = (15 2) th term – 2 nd term.

Comments are closed.