Fibonacci Numbers Definition Formula Fibonacci Series
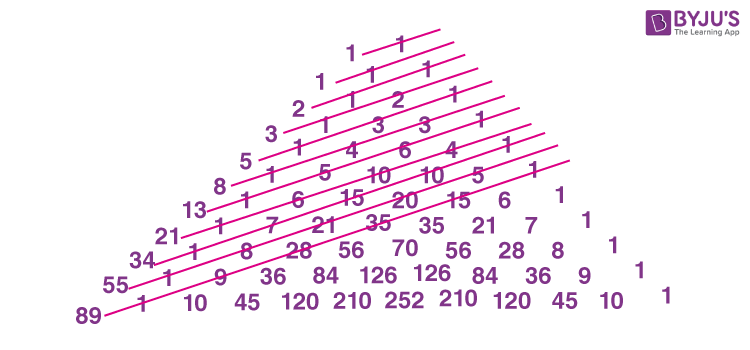
Fibonacci Numbers Definition Fibonacci Sequence Formula And Examples It means that if the pair of fibonacci numbers are of bigger value, then the ratio is very close to the golden ratio. so, with the help of golden ratio, we can find the fibonacci numbers in the sequence. the formula to calculate the fibonacci numbers using the golden ratio is: x n = [φ n – (1 φ) n] √5. where,. Fibonacci sequence. in mathematics, the fibonacci sequence is a sequence in which each number is the sum of the two preceding ones. numbers that are part of the fibonacci sequence are known as fibonacci numbers, commonly denoted fn . many writers begin the sequence with 0 and 1, although some authors start it from 1 and 1 [1][2] and some (as.

Fibonacci Sequence Definition Formula List Examples Diagrams Fibonacci numbers formula. the sequence of fibonacci numbers can be defined as: fn = fn 1 fn 2. where f n is the nth term or number. f n 1 is the (n 1)th term. f n 2 is the (n 2)th term. from the equation, we can summarize the definition as, the next number in the sequence, is the sum of the previous two numbers present in the sequence. Fibonacci sequence, the sequence of numbers 1, 1, 2, 3, 5, 8, 13, 21, …, each of which, after the second, is the sum of the two previous numbers. the numbers of the sequence occur throughout nature, and the ratios between successive terms of the sequence tend to the golden ratio. Solved examples. find the sum of the first 15 fibonacci numbers. solution: as we know, the sum of the fibonacci sequence = ∑ i = 0 n f i = f n 2 – f 2. = f n 2 − 1, where f n is the nth fibonacci number, and the sequence starts from f 0. thus, the sum of the first 15 fibonacci numbers = (15 2) th term – 2 nd term. Fibonacci sequence formula. the fibonacci sequence of numbers, say “fn” where the suffix n denotes the order or rank of term, is defined by. initial term: f 0 = 0. first term: f 1 = 1. these two terms together are known as the kick off part. formula for next terms: f n = f n − 1 f n − 2.
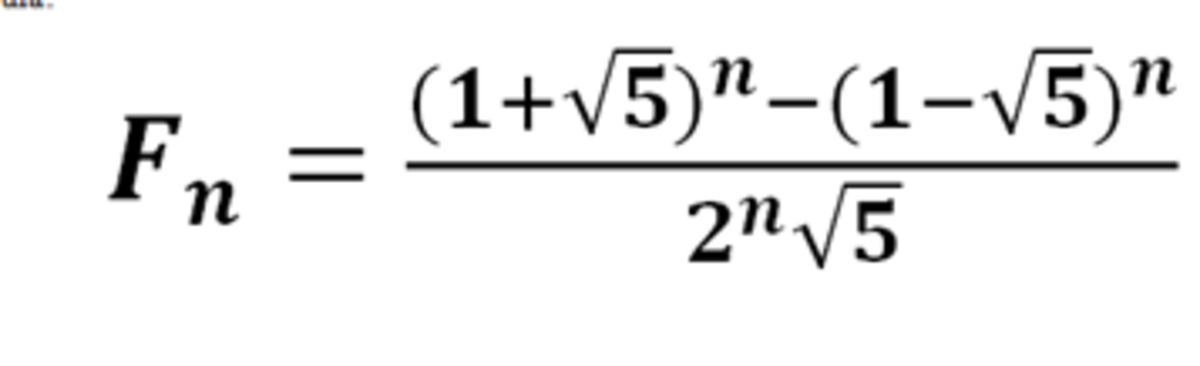
Fibonacci Sequence Formula Explained Images Solved examples. find the sum of the first 15 fibonacci numbers. solution: as we know, the sum of the fibonacci sequence = ∑ i = 0 n f i = f n 2 – f 2. = f n 2 − 1, where f n is the nth fibonacci number, and the sequence starts from f 0. thus, the sum of the first 15 fibonacci numbers = (15 2) th term – 2 nd term. Fibonacci sequence formula. the fibonacci sequence of numbers, say “fn” where the suffix n denotes the order or rank of term, is defined by. initial term: f 0 = 0. first term: f 1 = 1. these two terms together are known as the kick off part. formula for next terms: f n = f n − 1 f n − 2. Using the golden ratio to calculate fibonacci numbers. and even more surprising is that we can calculate any fibonacci number using the golden ratio: x n = φ n − (1−φ) n √5. the answer comes out as a whole number, exactly equal to the addition of the previous two terms. The fibonacci sequence has several interesting properties. 1) fibonacci numbers are related to the golden ratio. any fibonacci number can be calculated (approximately) using the golden ratio, f n = (Φ n (1 Φ) n) √5 (which is commonly known as "binet formula"), here φ is the golden ratio and Φ ≈ 1.618034.
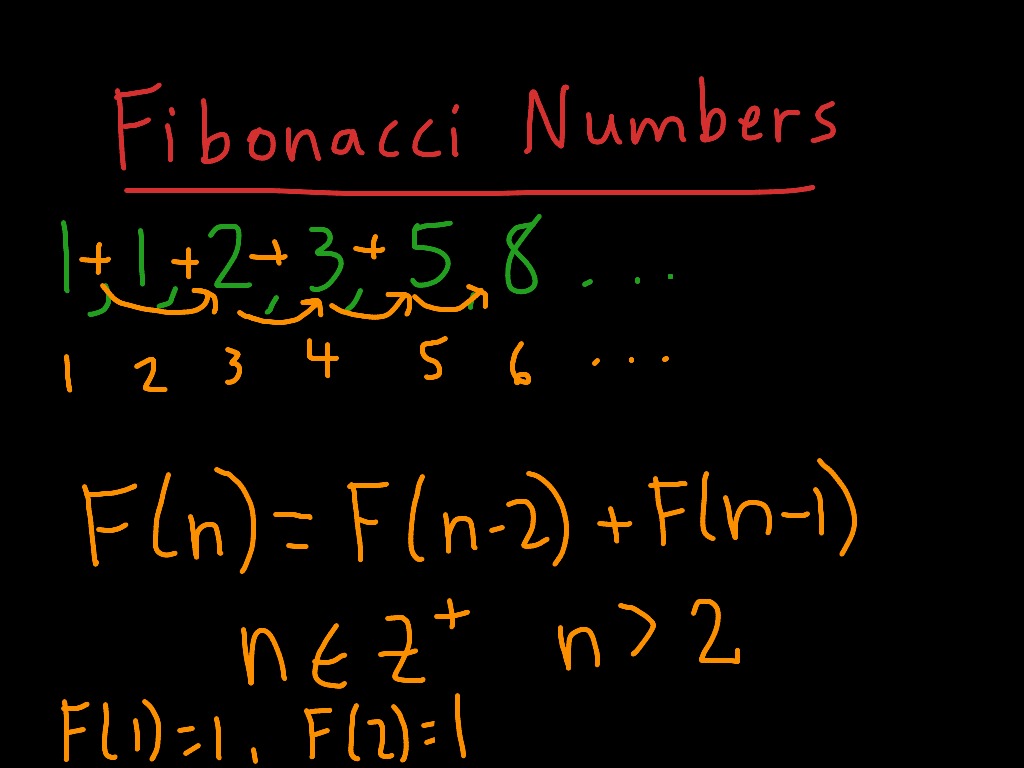
Fibonacci Numbers Definition Fibonacci Sequence Formula And Examples Images Using the golden ratio to calculate fibonacci numbers. and even more surprising is that we can calculate any fibonacci number using the golden ratio: x n = φ n − (1−φ) n √5. the answer comes out as a whole number, exactly equal to the addition of the previous two terms. The fibonacci sequence has several interesting properties. 1) fibonacci numbers are related to the golden ratio. any fibonacci number can be calculated (approximately) using the golden ratio, f n = (Φ n (1 Φ) n) √5 (which is commonly known as "binet formula"), here φ is the golden ratio and Φ ≈ 1.618034.

Fibonacci Numbers Definition Formula Fibonacci Series

Comments are closed.