Exterior Angle Theorem Triangles
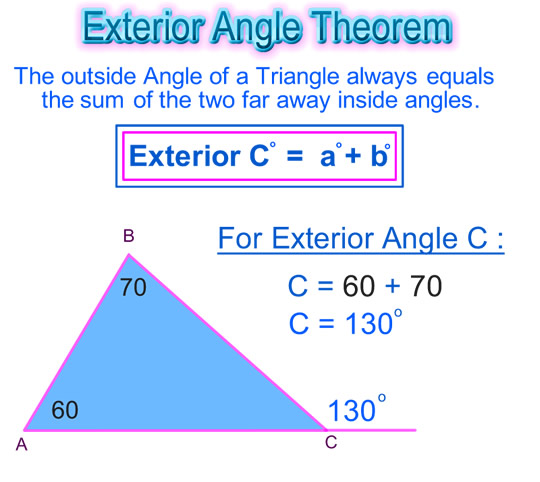
Exterior Angle Of A Triangle Passy S World Of Mathematics Exterior angle theorem. the exterior angle d of a triangle: equals the angles a plus b. is greater than angle a, and. is greater than angle b. example: the exterior angle is 35° 62° = 97°. and 97° > 35°. and 97° > 62°. Example 1: find the values of x and y by using the exterior angle theorem of a triangle. solution: ∠x is the exterior angle. ∠x 92 = 180º (linear pair of angles) ∠x = 180 92 = 88º. applying the exterior angle theorem, we get, ∠y 41 = 88. ∠y = 88 41 = 47º. therefore, the values of x and y are 88º and 47º respectively.
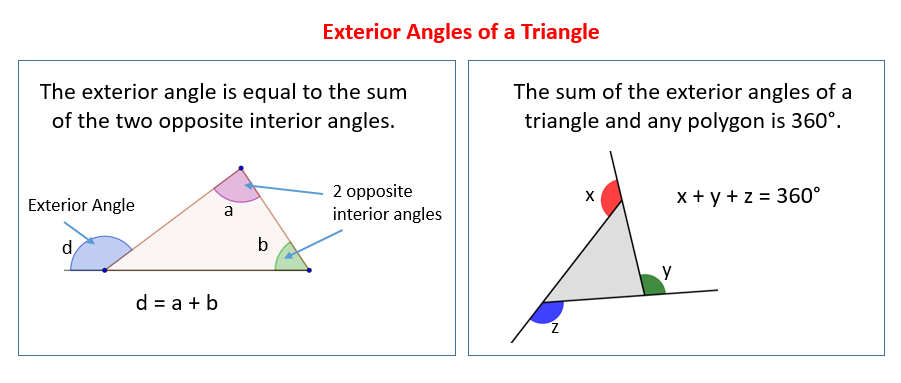
Exterior Angles Of A Triangle Video Lessons Examples Step By Step The above statement can be explained using the figure provided as: according to the exterior angle property of a triangle theorem, the sum of measures of ∠abc and ∠cab would be equal to the exterior angle ∠acd. general proof of this theorem is explained below: proof: consider a ∆abc as shown in fig. 2, such that the side bc of ∆abc is. The exterior angle theorem is proposition 1.16 in euclid's elements, which states that the measure of an exterior angle of a triangle is greater than either of the measures of the remote interior angles. this is a fundamental result in absolute geometry because its proof does not depend upon the parallel postulate. The exterior angle sum theorem states that the exterior angles of any polygon will always add up to 360 ∘. figure 4.18.3. m∠1 m∠2 m∠3 = 360 ∘. m∠4 m∠5 m∠6 = 360 ∘. the exterior angle theorem states that an exterior angle of a triangle is equal to the sum of its remote interior angles. (remote interior angles are the. According to the exterior angle theorem, ∠ b c d = ∠ a ∠ b. we can use this theorem to find the measure of an unknown angle in a triangle. example: find x. here, x is the exterior angle with two opposite interior angles measuring 55 ∘ and 45 ∘. by the exterior angle theorem, x = 55 ∘ 45 ∘ = 100 ∘.
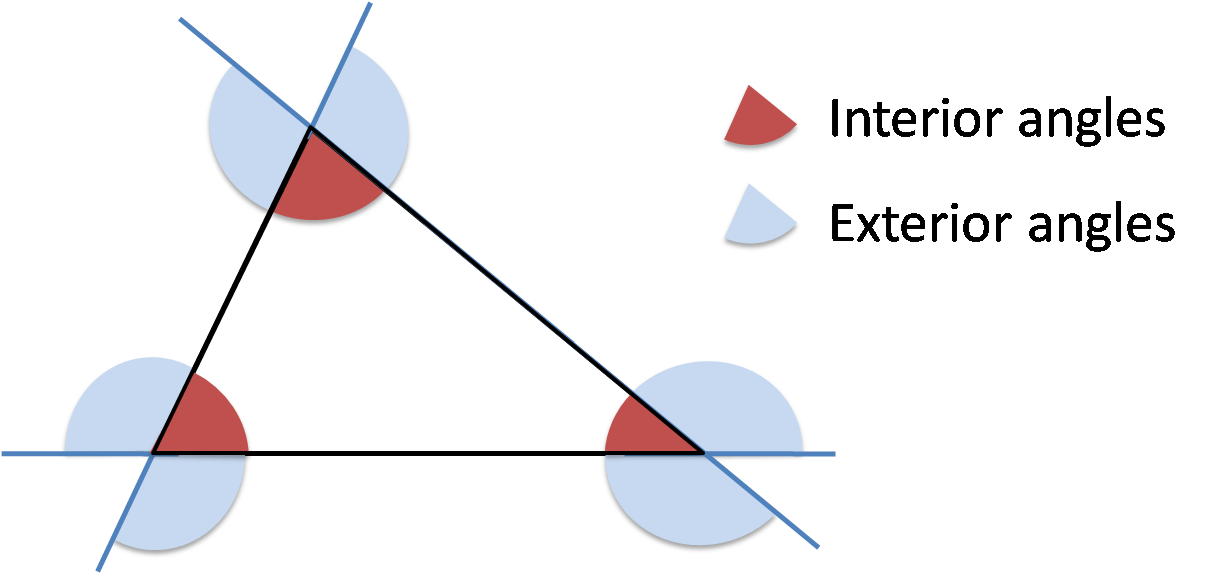
Triangle Angle Calculator Formula The exterior angle sum theorem states that the exterior angles of any polygon will always add up to 360 ∘. figure 4.18.3. m∠1 m∠2 m∠3 = 360 ∘. m∠4 m∠5 m∠6 = 360 ∘. the exterior angle theorem states that an exterior angle of a triangle is equal to the sum of its remote interior angles. (remote interior angles are the. According to the exterior angle theorem, ∠ b c d = ∠ a ∠ b. we can use this theorem to find the measure of an unknown angle in a triangle. example: find x. here, x is the exterior angle with two opposite interior angles measuring 55 ∘ and 45 ∘. by the exterior angle theorem, x = 55 ∘ 45 ∘ = 100 ∘. An exterior angle of a triangle is equal to the sum of the two opposite interior angles, thus an exterior angle is greater than any of its two opposite interior angles; for example, in Δabc, ∠5 = ∠a ∠b. the sum of an exterior angle and its adjacent interior angle is equal to 180 degrees; for example, ∠5 ∠c = 180°. Theorem: an exterior angle of a triangle is equal to the sum of the opposite interior angles. in the figure above, drag the orange dots on any vertex to reshape the triangle. the exterior angle at b is always equal to the opposite interior angles at a and c. although only one exterior angle is illustrated above, this theorem is true for any of.
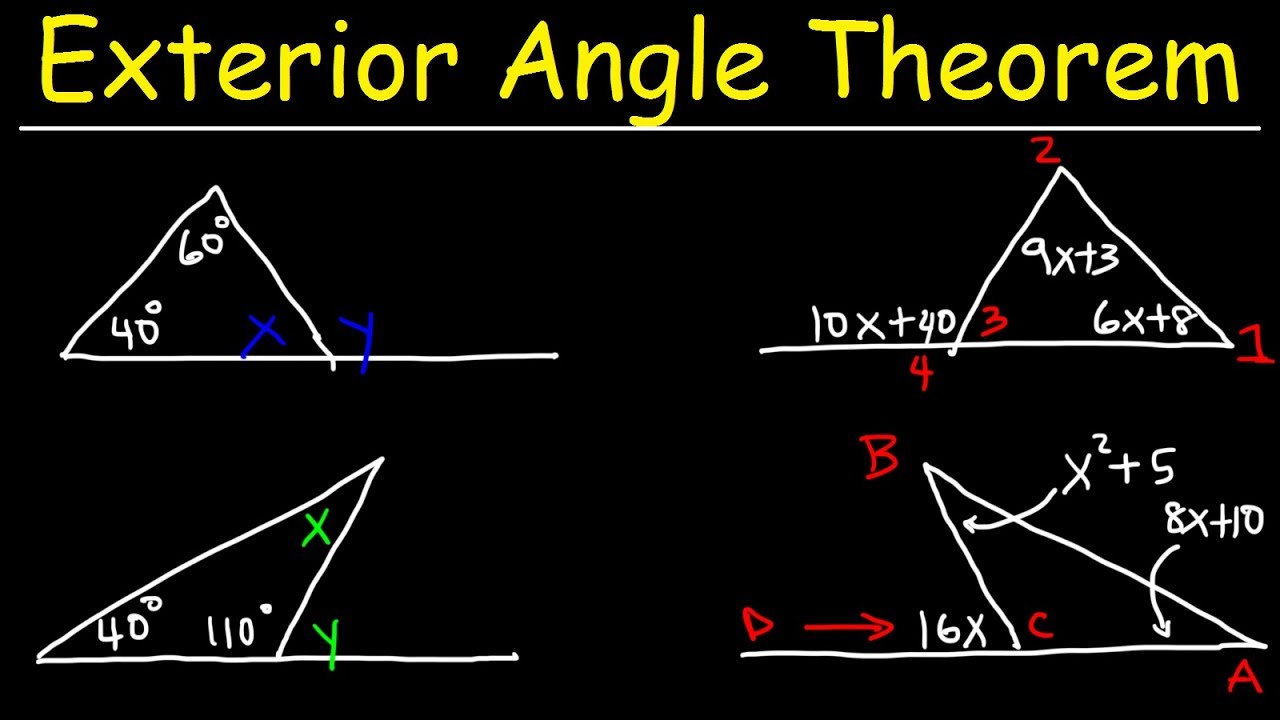
Exterior Angle Theorem For Triangles Practice Problems Geometry An exterior angle of a triangle is equal to the sum of the two opposite interior angles, thus an exterior angle is greater than any of its two opposite interior angles; for example, in Δabc, ∠5 = ∠a ∠b. the sum of an exterior angle and its adjacent interior angle is equal to 180 degrees; for example, ∠5 ∠c = 180°. Theorem: an exterior angle of a triangle is equal to the sum of the opposite interior angles. in the figure above, drag the orange dots on any vertex to reshape the triangle. the exterior angle at b is always equal to the opposite interior angles at a and c. although only one exterior angle is illustrated above, this theorem is true for any of.

Comments are closed.