Exterior Angle Theorem Definition Use Solved Examples

By gudangdomain On Nov 7, 2024 Last updated

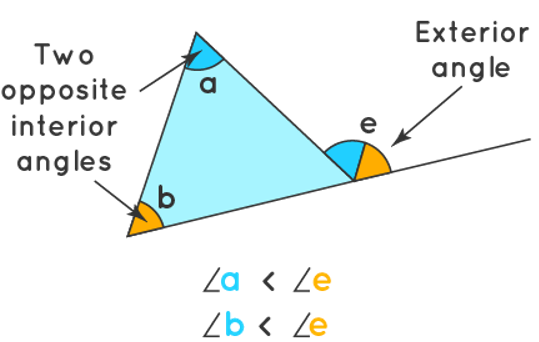
Exterior Angle Theorem Definition Use Solved Examples The exterior angle theorem states that when a triangle's side is extended, the resultant exterior angle formed is equal to the sum of the measures of the two opposite interior angles of the triangle. learn about exterior angle theorem statement, explanation, proof and solved examples. make your child a math thinker, the cuemath way!. Exterior angle theorem states that the measure of an exterior angle of a triangle is equal to the sum of two remote interior angles. the remote interior angles or opposite interior angles are the angles that are non adjacent with the exterior angle. a triangle is a polygon with three sides. when we extend any side of a triangle, an angle is.

Exterior Angle Theorem Definition Use Solved Examples Exterior angle theorem. the exterior angle d of a triangle: equals the angles a plus b. is greater than angle a, and. is greater than angle b. example: the exterior angle is 35° 62° = 97°. and 97° > 35°. and 97° > 62°. According to the exterior angle property of a triangle theorem, the sum of measures of ∠abc and ∠cab would be equal to the exterior angle ∠acd. general proof of this theorem is explained below: proof: consider a ∆abc as shown in fig. 2, such that the side bc of ∆abc is extended. a line, parallel to the side ab is drawn as shown in the. The exterior angle theorem states that: an exterior angle of a triangle is equal to the sum of the two opposite interior angles. the following diagram shows the exterior angle theorem. scroll down the page for more examples and solutions using the exterior angle theorem to solve problems. using the exterior angle theorem to solve problems. example:. Exterior angle theorem deals with the angle formed between a triangle’s side and its adjacent sides’ extended portion. the exterior angle formed is equal to the sum of the measures of both the opposite interior angles of the triangle. exterior angle theorem can be used to find the measure of an unknown angle in any triangle.

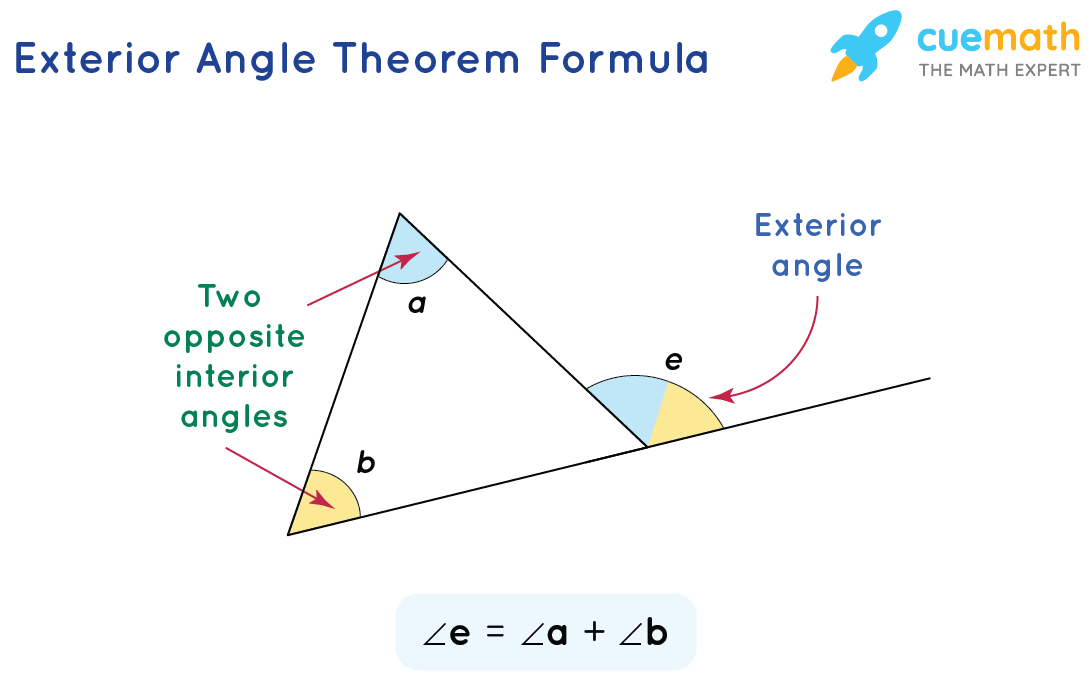
Exterior Angle Formula Concept And Solved Examples The exterior angle theorem states that: an exterior angle of a triangle is equal to the sum of the two opposite interior angles. the following diagram shows the exterior angle theorem. scroll down the page for more examples and solutions using the exterior angle theorem to solve problems. using the exterior angle theorem to solve problems. example:. Exterior angle theorem deals with the angle formed between a triangle’s side and its adjacent sides’ extended portion. the exterior angle formed is equal to the sum of the measures of both the opposite interior angles of the triangle. exterior angle theorem can be used to find the measure of an unknown angle in any triangle. This video explains the exterior angle theorem of geometry. the theorem is used to work out some applications in finding angles of a triangle. exterior angle theorem. students learn the exterior angle theorem, which states that the exterior angle of a triangle is equal to the sum of the measures of the remote interior angles. This video explains the exterior angle theorem of geometry. the theorem is used to work out some applications in finding angles of a triangle. students learn the exterior angle theorem, which states that the exterior angle of a triangle is equal to the sum of the measures of the remote interior angles. students are then asked to solve problems.

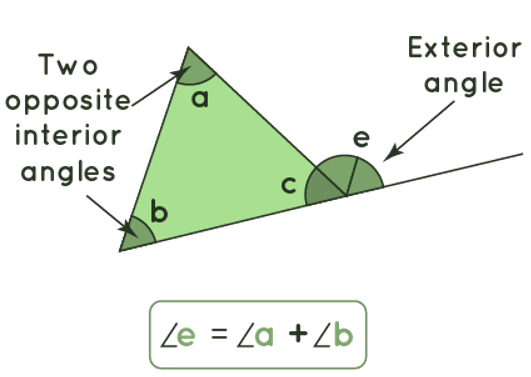
Exterior Angle Theorem Definition Use Solved Examples This video explains the exterior angle theorem of geometry. the theorem is used to work out some applications in finding angles of a triangle. exterior angle theorem. students learn the exterior angle theorem, which states that the exterior angle of a triangle is equal to the sum of the measures of the remote interior angles. This video explains the exterior angle theorem of geometry. the theorem is used to work out some applications in finding angles of a triangle. students learn the exterior angle theorem, which states that the exterior angle of a triangle is equal to the sum of the measures of the remote interior angles. students are then asked to solve problems.

Uncover Hidden Gems and Plan Your Dream Getaways: Get inspired to travel the world with our Exterior Angle Theorem Definition Use Solved Examples guides. From awe-inspiring destinations to insider travel tips, we'll help you plan unforgettable journeys and create lifelong memories.

Exterior Angle Theorem For Triangles, Practice Problems - Geometry

Exterior Angle Theorem For Triangles, Practice Problems - Geometry Exterior Angle Theorem — Formula & Examples Exterior Angle Theorem (Triangles) Exterior Angles Theorem - Solve for X | Geometry | Eat Pi Angles of Triangle: Sum of Interior Angles and Exterior Angle Theorem by @MathTeacherGon Find the Measure of the EXTERIOR ANGLE | Triangle Exterior Angle Theorem | Geometry Exterior Angle Theorem How to Use the Exterior Angle Theorem In Solving for a Missing Angle of A Triangle Unraveling the Mystery of Circles: Exploring Family, Angle between Circles & Orthogonal Circles! Exterior Angle Theorem: How to find the measure of Angles? Exterior angle theorem proof and solved examples EXTERIOR ANGLE THEOREM | Use the Exterior Angle Theorem to Find X | Geometry Exterior Angle Theorem for Triangles Exterior Angle Theorem Tutorial Exterior Angle Theorem Exterior Angle Theorem by @MathTeacherGon Exterior and Remote Interior Angles by Shmoop G9Adv 17 Prove the Exterior Angle Theorem and apply the theorem to solve problems Proving the Exterior Angle Theorem Trianlge Sum and Exterior Angle Theorem

Conclusion

Taking a closer look at the subject, there is no doubt that this particular post presents useful information in connection with Exterior Angle Theorem Definition Use Solved Examples. Throughout the content, the blogger illustrates remarkable understanding in the field. Markedly, the analysis of Z stands out as a highlight. Furthermore, the post performs admirably in disentangling complex concepts in an simple manner. Also, the creator gives case studies that bring the concepts to life. A further aspect that differentiates this write-up is the comprehensive analysis of diverse aspects related to Exterior Angle Theorem Definition Use Solved Examples. The essayists detailed technique guarantees that spectators get a complete picture of the subject matter. Thanks for considering this write-up. If theres anything else youd like to know, you are welcome to reach out through any social network. I am eager to your reactions. In final remarks, as you continue exploring, noted below are some connected compositions that you will find insightful:May you find them engaging!