Exponential Derivative Visual

Calculus Exponential Derivatives Examples Solutions Videos Derivatives of exponential functions. in order to differentiate the exponential function. f (x) = a^x, f (x) = ax, we cannot use power rule as we require the exponent to be a fixed number and the base to be a variable. instead, we're going to have to start with the definition of the derivative: \begin {aligned} f' (x) &= \lim {h \rightarrow 0. Derivative of exponential function examples. example 1: find the derivative of exponential function f (x) = 3 x 3x 2. solution: using the formula for derivative of exponential function and other differentiation formulas, the derivative of f (x) = 3 x 3x 2 is given by, f' (x) = 3 x ln 3 6x.
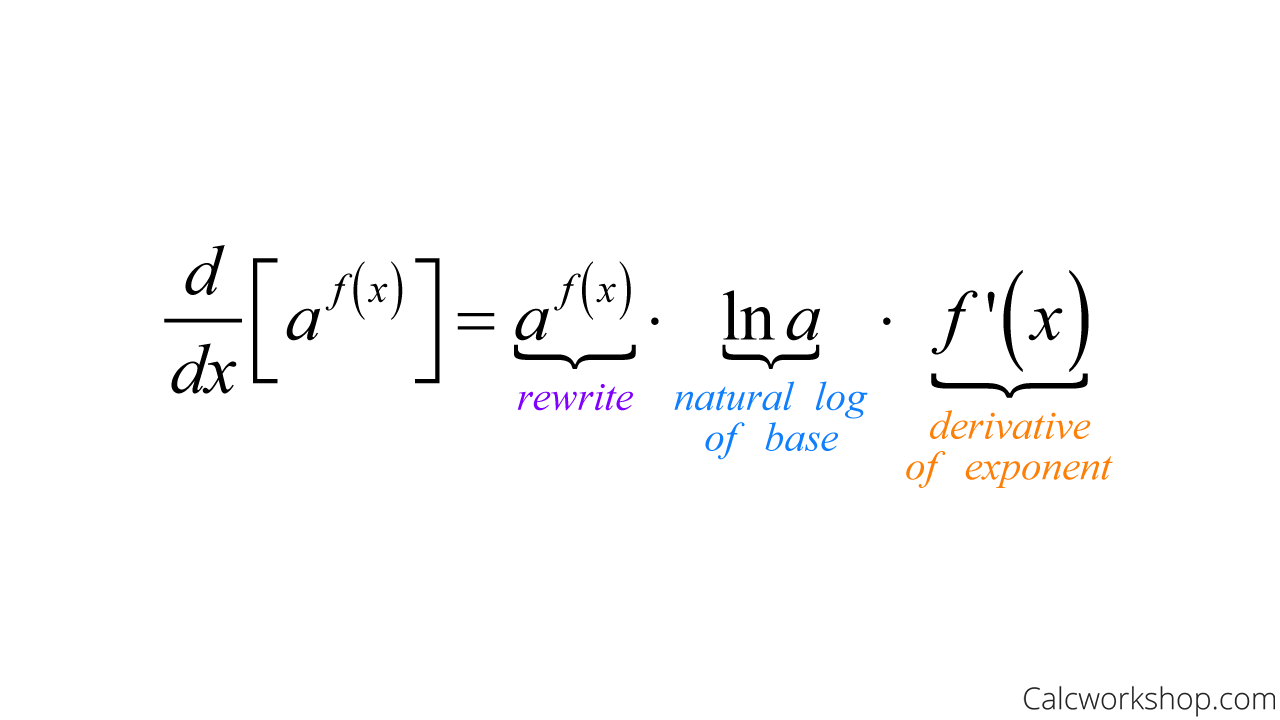
Derivative Of Exponential Function Fully Explained A visual of the derivative of f(x)=e^x. we show how to think about the derivative of a function visually. #manim #calculus #derivatives #derivative #tangentl. The function e(x) = ex is called the natural exponential function. its inverse, l(x) = logex = lnx is called the natural logarithmic function. figure 3.33 the graph of e(x) = ex is between y = 2x and y = 3x. for a better estimate of e, we may construct a table of estimates of b ′ (0) for functions of the form b(x) = bx. You can use the slider for b to change the base of the exponential function f(x) = b^x and see the relationship between the function f in red, and its derivative df dx in green. 2 expression 3: "f" left parenthesis, "x" , right parenthesis equals "b" superscript, "x" , baseline f x = b x. The exponential function f (x) = e x has the property that it is its own derivative. this means that the slope of a tangent line to the curve y = e x at any point is equal to the y coordinate of the point. we can combine the above formula with the chain rule to get. example: differentiate the function y = e sin x.

Exponential Derivative Visual Youtube You can use the slider for b to change the base of the exponential function f(x) = b^x and see the relationship between the function f in red, and its derivative df dx in green. 2 expression 3: "f" left parenthesis, "x" , right parenthesis equals "b" superscript, "x" , baseline f x = b x. The exponential function f (x) = e x has the property that it is its own derivative. this means that the slope of a tangent line to the curve y = e x at any point is equal to the y coordinate of the point. we can combine the above formula with the chain rule to get. example: differentiate the function y = e sin x. 6. derivative of the exponential function. by m. bourne. the derivative of e x is quite remarkable. the expression for the derivative is the same as the expression that we started with; that is, e x! `(d(e^x)) (dx)=e^x` what does this mean? it means the slope is the same as the function value (the y value) for all points on the graph. See, differentiating exponential functions is a snap — it’s as easy as 1 2 3! is derived from a. this video lesson will look at exponential properties and how to take a derivative of an exponential function, all while walking through several examples in detail. let’s jump right in. video tutorial w full lesson & detailed examples (video).

Derivative Of Exponential Function Formula Proof Examples 6. derivative of the exponential function. by m. bourne. the derivative of e x is quite remarkable. the expression for the derivative is the same as the expression that we started with; that is, e x! `(d(e^x)) (dx)=e^x` what does this mean? it means the slope is the same as the function value (the y value) for all points on the graph. See, differentiating exponential functions is a snap — it’s as easy as 1 2 3! is derived from a. this video lesson will look at exponential properties and how to take a derivative of an exponential function, all while walking through several examples in detail. let’s jump right in. video tutorial w full lesson & detailed examples (video).

Comments are closed.