Exponent Rules With Examples

Exponent Rules And Examples Laws of exponents. exponents are also called powers or indices. the exponent of a number says how many times to use the number in a multiplication. in this example: 82 = 8 × 8 = 64. in words: 8 2 could be called "8 to the second power", "8 to the power 2" or simply "8 squared". try it yourself:. According to the exponent rules, to multiply two expressions with the same base, we add the exponents while the base remains the same. this means, 10 3 × 10 4 = 10 ( 3 4) = 10 1 = 10. answer: 10. example 2: simplify the given expression and select the correct option using the laws of exponents: 10 15 ÷ 10 7. (a) 10 8.
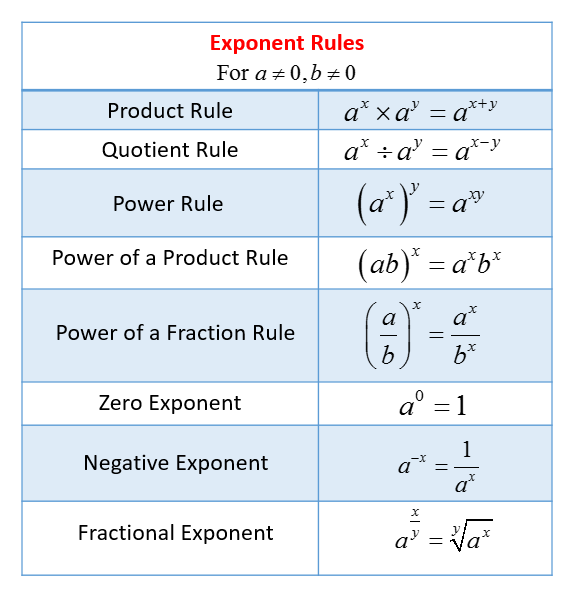
Exponent Rules Video Lessons Examples And Solutions There are many different laws of exponents. this page covers the 3 most frequently studied laws of exponents (rules 1 3 below). rule 1: $$ \boxed{ x^a \cdot x^ b = x^{a \red b} } \\ \text{example : } \\ 3^4 \cdot 3^2 = 3^{4 2} \\ 3^4 \cdot 3^2 = 3^{6} $$. Some of the examples are: 3 4 = 3×3×3×3. 10 5 = 10×10×10×10×10. 16 3 = 16 × 16 × 16. suppose, a number ‘a’ is multiplied by itself n times, then it is represented as a n where a is the base and n is the exponent. exponents follow certain rules that help in simplifying expressions which are also called its laws. Now, let’s go over the seven (7) basic exponent rules or laws. any nonzero number raised to zero power is equal to 1. we have a nonzero base of , and an exponent of zero. the zero rule of exponent can be directly applied here. thus, {5^0} = 1. the base here is the entire expression inside the parenthesis, and the good thing is that it is. Step by step guide: multiplying exponents. 2 power of a quotient rule: dividing exponents. when dividing exponents with the same base, use subtraction to subtract the powers. a^ {m} \div a^ {n}=a^ {m n} am ÷an = am−n. step by step guide: dividing exponents. 3 negative exponent rule.

Exponent Rules Laws Of Exponents Exponent Rules Chart Now, let’s go over the seven (7) basic exponent rules or laws. any nonzero number raised to zero power is equal to 1. we have a nonzero base of , and an exponent of zero. the zero rule of exponent can be directly applied here. thus, {5^0} = 1. the base here is the entire expression inside the parenthesis, and the good thing is that it is. Step by step guide: multiplying exponents. 2 power of a quotient rule: dividing exponents. when dividing exponents with the same base, use subtraction to subtract the powers. a^ {m} \div a^ {n}=a^ {m n} am ÷an = am−n. step by step guide: dividing exponents. 3 negative exponent rule. Base (second term): 6 6. exponent: (first term): 5 5. exponent: (second term): 3 3. apply the appropriate exponent rule (s) according to the operation. show step. since you are dividing two numbers with the same base, you can use the quotient rule which says to subtract the exponents: am÷an =am−n am ÷ an = am−n. Let’s simplify 52 and the exponent is 4, so you multiply (52)4 = 52 ⋅ 52 ⋅ 52 ⋅ 52 = 58 (using the product rule—add the exponents). 58. notice that the new exponent is the same as the product of the original exponents: 2 ⋅ 4 = 8. so, (52)4 = 52 ⋅ 4 = 58 (which equals 390,625, if you do the multiplication).

Exponents Inb Pages Mrs E Teaches Math Base (second term): 6 6. exponent: (first term): 5 5. exponent: (second term): 3 3. apply the appropriate exponent rule (s) according to the operation. show step. since you are dividing two numbers with the same base, you can use the quotient rule which says to subtract the exponents: am÷an =am−n am ÷ an = am−n. Let’s simplify 52 and the exponent is 4, so you multiply (52)4 = 52 ⋅ 52 ⋅ 52 ⋅ 52 = 58 (using the product rule—add the exponents). 58. notice that the new exponent is the same as the product of the original exponents: 2 ⋅ 4 = 8. so, (52)4 = 52 ⋅ 4 = 58 (which equals 390,625, if you do the multiplication).

Comments are closed.