Examples Of Properties Of Real Numbers
Properties Of Real Numbers Examples Solutions Worksheets Videos Properties of real numbers mathbitsnotebook (a1) a real number is a value that represents a quantity along a continuous number line. real numbers can be ordered. the symbol for the set of real numbers is , which is the letter r in the typeface "blackboard bold". the real numbers include: counting (natural) numbers () {1, 2, 3,. Closure example. a b is real 2 3 = 5 is real. a×b is real 6 × 2 = 12 is real . adding zero leaves the real number unchanged, likewise for multiplying by 1: identity example. a 0 = a 6 0 = 6. a × 1 = a 6 × 1 = 6 . for addition the inverse of a real number is its negative, and for multiplication the inverse is its reciprocal: additive.

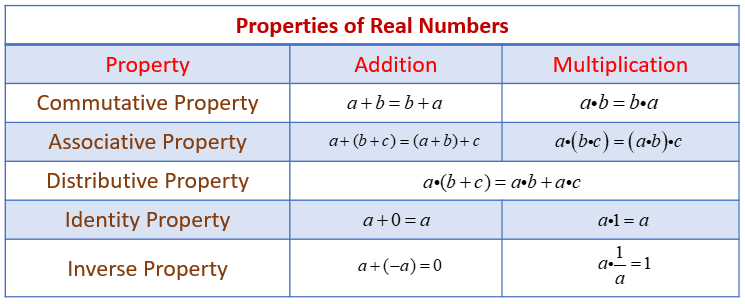
Properties Of Real Numbers Teach Math Interactive Commutative property. of addition if a and bare real numbers, then a b = b a. of multiplication if a and bare real numbers, then a · b = b · a. when adding or multiplying, changing the order gives the same result. the commutative property has to do with order. we subtract 9 − 8 and 8 − 9, and see that 9 − 8 ≠ 8 − 9. At the same time, the imaginary numbers are the un real numbers, which cannot be expressed in the number line and are commonly used to represent a complex number. some of the examples of real numbers are 23, 12, 6.99, 5 2, π, and so on. To keep it organized, i decided to divide the properties of real numbers into three (3) parts. the first one involves the addition operation. the second involves the operation of multiplication. while the third combines the operations of addition and multiplication. verbal description: if you add two real numbers, the sum is also a real number. The inverse properties: 1. if a is any real number, then there is a unique real number − a, such that. a (− a) = 0 and − a a = 0. the numbers a and − a are called additive inverses of each other. 2. if a is any nonzero real number, then there is a unique real number 1 a such that. a ⋅ 1 a = 1 and 1 a ⋅ a = 1.

Ppt 1 1 Properties Of Real Numbers Powerpoint Presentation Free To keep it organized, i decided to divide the properties of real numbers into three (3) parts. the first one involves the addition operation. the second involves the operation of multiplication. while the third combines the operations of addition and multiplication. verbal description: if you add two real numbers, the sum is also a real number. The inverse properties: 1. if a is any real number, then there is a unique real number − a, such that. a (− a) = 0 and − a a = 0. the numbers a and − a are called additive inverses of each other. 2. if a is any nonzero real number, then there is a unique real number 1 a such that. a ⋅ 1 a = 1 and 1 a ⋅ a = 1. A number and its reciprocal multiply to one. 1 a is the multiplicative inverse of a. properties of zero. for any real number a, a ⋅ 0 = 0 0 · a = 0 – the product of any real number and 0 is 0. 0 a = 0 for a ≠ 0 – zero divided by any real number except zero is zero. a 0 is undefined – division by zero is undefined. Scroll down the page for more examples and solutions using the properties of real numbers. properties of real numbers defines the properties of real numbers and then provides examples of the properties by rewriting and simplifying expressions.these include the distributive property, factoring, the inverse properties, the identity properties.

Properties Of Real Numbers Welcome To Ms Gillen S Class A number and its reciprocal multiply to one. 1 a is the multiplicative inverse of a. properties of zero. for any real number a, a ⋅ 0 = 0 0 · a = 0 – the product of any real number and 0 is 0. 0 a = 0 for a ≠ 0 – zero divided by any real number except zero is zero. a 0 is undefined – division by zero is undefined. Scroll down the page for more examples and solutions using the properties of real numbers. properties of real numbers defines the properties of real numbers and then provides examples of the properties by rewriting and simplifying expressions.these include the distributive property, factoring, the inverse properties, the identity properties.

Real Numbers Definition Symbol Properties Chart Examples

Comments are closed.