Example 5 If A Transversal Intersects Two Lines Such That Examples

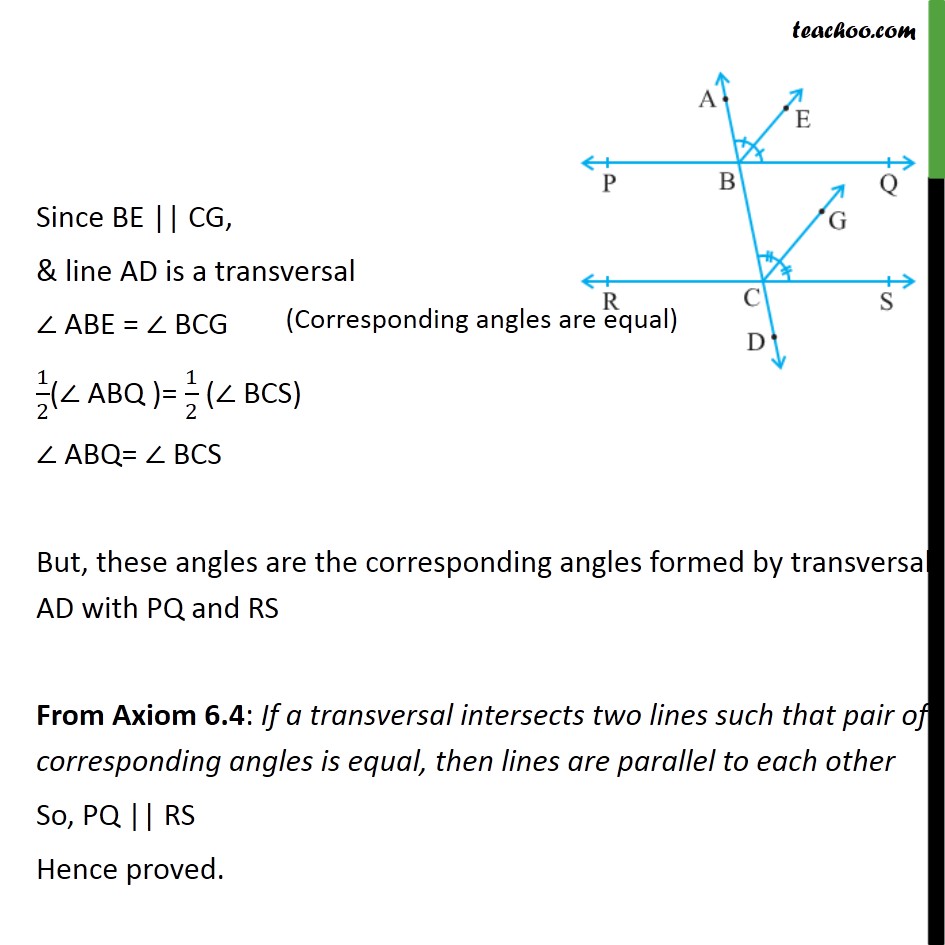
Example 5 If A Transversal Intersects Two Lines Such That Transcript. example 5 if a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel. in figure, transversal ad intersects two lines pq and rs at points b and c respectively. ray be is the bisector of bacq so , abe = ebq = 1 2 ( abq ) and ray cg is the. A transversal is defined as a line that passes through two lines in the same plane at two distinct points in the geometry. a transversal intersection with two lines produces various types of angles in pairs, such as consecutive interior angles, corresponding angles and alternate angles. a transversal produces 8 angles and this can be observed.

Example 5 If A Transversal Intersects Two Lines Such That Examples A transversal is any line that intersects two straight lines at distinct points. a transversal that cuts the lines l 1 and l 2 is the transversal line. intersection caused by transversals forms several angles. these are: a) corresponding angles b) alternate interior angles c) alternate exterior angles d) co interior angles; related articles on. Angles, parallel lines, & transversals. parallel lines are lines in the same plane that go in the same direction and never intersect. when a third line, called a transversal, crosses these parallel lines, it creates angles. some angles are equal, like vertical angles (opposite angles) and corresponding angles (same position at each intersection). We will now go on to the specific case of two parallel lines being cut by a transversal. the following are the properties of the 8 angles so formed. all the corresponding angles are equal. ∠1 = ∠5. ∠2 = ∠6. ∠4 = ∠8. ∠3 = ∠7. all the alternate interior angles are equal. ∠3 = ∠5. Various theorems are defined for transversal, such as: 1. if a transversal intersects two parallel lines, then each pair of corresponding angles is equal. 2. if a transversal intersects two lines such that a pair of corresponding angles are equal, then the two lines are parallel to each other. 3.

Transversal Lines We will now go on to the specific case of two parallel lines being cut by a transversal. the following are the properties of the 8 angles so formed. all the corresponding angles are equal. ∠1 = ∠5. ∠2 = ∠6. ∠4 = ∠8. ∠3 = ∠7. all the alternate interior angles are equal. ∠3 = ∠5. Various theorems are defined for transversal, such as: 1. if a transversal intersects two parallel lines, then each pair of corresponding angles is equal. 2. if a transversal intersects two lines such that a pair of corresponding angles are equal, then the two lines are parallel to each other. 3. In geometry, a transversal is a line that intersects two or more other (often parallel ) lines. in the figure below, line n is a transversal cutting lines l and m . when two or more lines are cut by a transversal, the angles which occupy the same relative position are called corresponding angles . in the figure the pairs of corresponding angles. Alternate interior angles are formed when a transversal crosses two parallel or non parallel lines. one way to help you identify this angle pair is to look closely at the words alternate and interior. in our diagram above, both are located on the inner side or in between the lines . they are also on opposite sides of the transversal and are not.