Ex 6 Integration Using Trigonometric Substitution Youtube This video provides an example of how to determine an indefinite integral using trigonometric substitution.site: mathispower4u. This video explains how to find an indefinite integral involving an inverse trigonometric function using u substitution.site: mathispower4u.
Trigonometric Substitution 6 Integral Calculus Youtube Integrate using trigo substitution int dx (sqrt (x^2 4x))^3 ? by changing variables, integration can be simplified by using the substitutions x=a\sin (\theta), x=a\tan (\theta), or x=a\sec (\theta). once the substitution is made the function can be simplified using basic trigonometric identities. Trigonometric substitutions are a specific type of u u substitutions and rely heavily upon techniques developed for those. they use the key relations \sin^2x \cos^2x = 1 sin2 x cos2 x = 1, \tan^2x 1 = \sec^2x tan2 x 1 = sec2 x, and \cot^2x 1 = \csc^2x cot2 x 1 = csc2 x to manipulate an integral into a simpler form. Figure 7.3.7: calculating the area of the shaded region requires evaluating an integral with a trigonometric substitution. we can see that the area is a = ∫5 3√x2 − 9dx. to evaluate this definite integral, substitute x = 3secθ and dx = 3secθtanθdθ. we must also change the limits of integration. Lesson objectives. recognize the binomials that lend themselves to trigonometric substitutions. complete the square in order to re write a quadratic polynomial in the form of a trigonometric substitution binomial. evaluate integrals using trigonometric substitution.
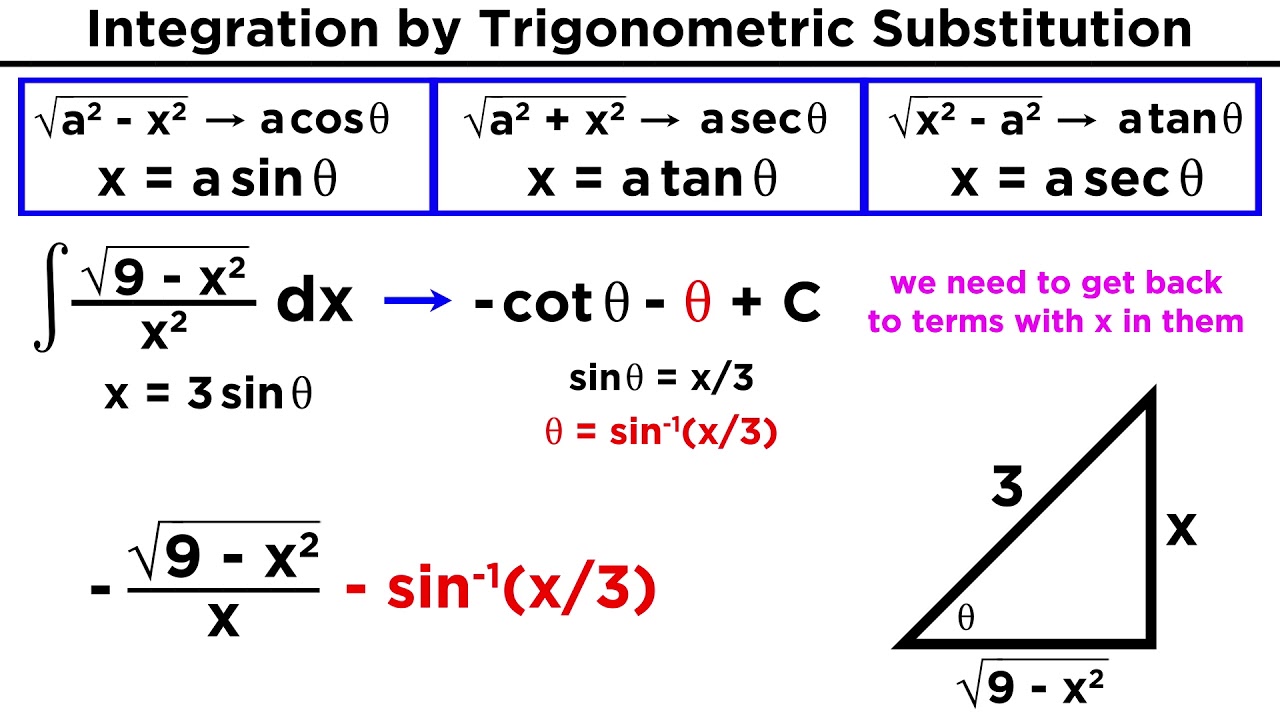
Integration By Trigonometric Substitution Youtube Figure 7.3.7: calculating the area of the shaded region requires evaluating an integral with a trigonometric substitution. we can see that the area is a = ∫5 3√x2 − 9dx. to evaluate this definite integral, substitute x = 3secθ and dx = 3secθtanθdθ. we must also change the limits of integration. Lesson objectives. recognize the binomials that lend themselves to trigonometric substitutions. complete the square in order to re write a quadratic polynomial in the form of a trigonometric substitution binomial. evaluate integrals using trigonometric substitution. Examples of such expressions are $$ \displaystyle{ \sqrt{ 4 x^2 }} \ \ \ and \ \ \ \displaystyle{(x^2 1)^{3 2}} $$ the method of trig substitution may be called upon when other more common and easier to use methods of integration have failed. trig substitution assumes that you are familiar with standard trigonometric identies, the use of. This video provides an example of how to determine an indefinite integral using trigonometric substitution and completing the square.site: mathispower.
Comments are closed.