Euclid S Elements Book I Proposition 9 To Bisect A Given Angle

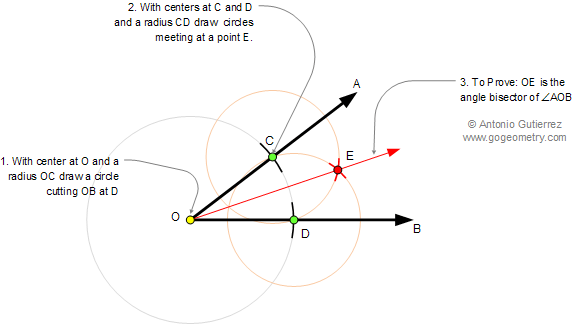
Euclid S Elements Book I Proposition 9 To Bisect A Given Angle Book i. propositions 9 and 10. we will now solve the problem of bisecting an angle, that is, dividing it into two equal angles, and of bisecting a straight line. place the point of the compass on a, and swing an arc ed. then, with d as center and de as radius, draw an arc. keeping the same radius and with e as center, draw an arc that will. It is required to bisect it. i.3. i.post.1, i.1. take an arbitrary point d on ab. cut off ae from ac equal to ad, and join de. construct the equilateral triangle def on de, and join af. i say that the angle bac is bisected by the straight line af. since ad equals ae, and af is common, therefore the two sides ad and af equal the two sides ea and.

How To Bisect An Angle Euclid Elements Book 1 Proposition 9 Youtube Check out my new website: eulersacademy.orgthis is the ninth proposition in euclid's first book of the elements. this proof is a construction that allows. Proposition 9. to bisect a given rectilineal angle. let the angle bac be the given rectilineal angle. thus it is required to bisect it. let a point d be taken at random on ab; let ae be cut off from ac equal to ad; [i. 3] let de be joined, and on de let the equilateral triangle def be constructed; let af be joined. Proposition 9. to bisect a given rectilinear angle. proposition 10. to bisect a given finite straight line. proposition 11. to draw a straight line at right angles to a given straight line from a given point on it. proposition 12. to draw a straight line perpendicular to a given infinite straight line from a given point not on it. proposition 13. The elements: books i xiii euclid's elements is the oldest mathematical and geometric treatise consisting of 13 books written by euclid in alexandria c. 300 bc. it is a collection of definitions, postulates, axioms, 467 propositions (theorems and constructions), and mathematical proofs of the propositions.

Math On The Mckenzie Euclid S Elements Book 1 Proposition 9 To Bisect Proposition 9. to bisect a given rectilinear angle. proposition 10. to bisect a given finite straight line. proposition 11. to draw a straight line at right angles to a given straight line from a given point on it. proposition 12. to draw a straight line perpendicular to a given infinite straight line from a given point not on it. proposition 13. The elements: books i xiii euclid's elements is the oldest mathematical and geometric treatise consisting of 13 books written by euclid in alexandria c. 300 bc. it is a collection of definitions, postulates, axioms, 467 propositions (theorems and constructions), and mathematical proofs of the propositions. Proposition 9 of book i of euclid’s elements of geometry establishes the feasibility of bisecting a rectilineal angle. euclid assumes, from the earlier propositions of book i of the elements, the following propositions: proposition 1, which establishes the possibility of constructing an equilateral triangle with a given line segment as one of. To bisect a given rectilineal angle. (the elements: book $\text{i}$: proposition $9$) this proof is proposition $9$ of book $\text{i}$ of euclid's the elements.