Euclid S Elements Book I Proposition 9
Math On The Mckenzie Euclid S Elements Book 1 Proposition 9 To Bisect Also, line bisection is quite easy (see the next proposition i.10), and division of a line into any number of equal parts is not especially difficult (see proposition vi.9). dividing an angle into an odd number of equal parts is not so easy, in fact, it is impossible to trisect a 60° angle using euclidean tools (the postulates 1 through 3). Proposition 9. to bisect a given rectilineal angle. let the angle bac be the given rectilineal angle. thus it is required to bisect it. let a point d be taken at random on ab; let ae be cut off from ac equal to ad; [i. 3] let de be joined, and on de let the equilateral triangle def be constructed; let af be joined.

Euclid S Elements Book 1 Proposition 9 Youtube Proclus (p. 357, 9) explains that euclid uses the word alternate (or, more exactly, alternately, ἐναλλάξ) in two connexions, (1) of a certain transformation of a proportion, as in book v. and the arithmetical books, (2) as here, of certain of the angles formed by parallels with a straight line crossing them. Euclid. euclid's elements. sir thomas little heath. new york. dover. 1956. the national science foundation provided support for entering this text. purchase a copy of this text (not necessarily the same edition) from amazon. The elements (greek: Στοιχεῖα stoikheîa) is a mathematical treatise consisting of 13 books attributed to the ancient greek mathematician euclid c. 300 bc. it is a collection of definitions, postulates, propositions (theorems and constructions), and mathematical proofs of the propositions. the books cover plane and solid euclidean. That agrees with euclid’s definition of them in i.def.9 and i.def.8. also in book iii, parts of circumferences of circles, that is, arcs, appear as magnitudes. only arcs of equal circles can be compared or added, so arcs of equal circles comprise a kind of magnitude, while arcs of unequal circles are magnitudes of different kinds.

Euclid S Elements Book 1 Proposition 9 Bisecting An Angle Youtube The elements (greek: Στοιχεῖα stoikheîa) is a mathematical treatise consisting of 13 books attributed to the ancient greek mathematician euclid c. 300 bc. it is a collection of definitions, postulates, propositions (theorems and constructions), and mathematical proofs of the propositions. the books cover plane and solid euclidean. That agrees with euclid’s definition of them in i.def.9 and i.def.8. also in book iii, parts of circumferences of circles, that is, arcs, appear as magnitudes. only arcs of equal circles can be compared or added, so arcs of equal circles comprise a kind of magnitude, while arcs of unequal circles are magnitudes of different kinds. Book i propositions proposition 1. on a given finite straight line to construct an equilateral triangle. proposition 2. to place at a given point (as an extremity) a straight line equal to a given straight line. proposition 3. given two unequal straight lines, to cut off from the greater a straight line equal to the less. proposition 4. Euclid:proposition i 9. from proofwiki. jump to navigation jump to search. to bisect a given rectilineal angle. (the elements: book $\text{i}$: proposition $9.
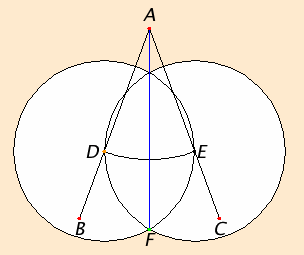
Euclid S Elements Book I Proposition 9 Book i propositions proposition 1. on a given finite straight line to construct an equilateral triangle. proposition 2. to place at a given point (as an extremity) a straight line equal to a given straight line. proposition 3. given two unequal straight lines, to cut off from the greater a straight line equal to the less. proposition 4. Euclid:proposition i 9. from proofwiki. jump to navigation jump to search. to bisect a given rectilineal angle. (the elements: book $\text{i}$: proposition $9.
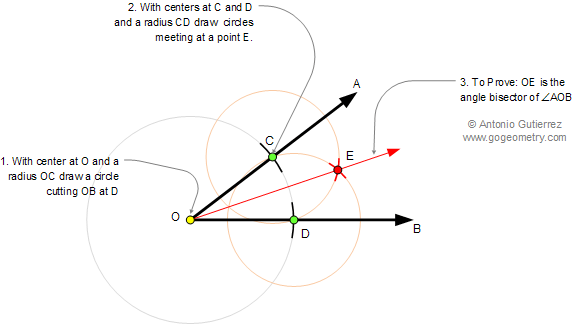
Euclid S Elements Book I Proposition 9 To Bisect A Given Angle

Euclid S Elements Book 1 Propositions 8 And 9 Youtube

Comments are closed.