Euclid I 3 Euclid Elements Book I Proposition 3

Euclid S Elements Index Online Geometry Tutor Elearning College Now it is clear that the purpose of proposition 2 is to effect the construction in this proposition. according to proclus (410–485 c.e.) in his commentary on book i, hippocrates of chios (fl. ca. 430 b.c.e.) was the first to write an elements. leon and theudius also wrote versions before euclid (fl. ca. 295 b.c.e.). Proposition 3. given two unequal straight lines, to cut off from the greater a straight line equal to the less. let ab, c be the two given unequal straight lines, and let ab be the greater of them. thus it is required to cut off from ab the greater a straight line equal to c the less. at the point a let ad be placed equal to the straight line c.

Euclid S Elements Book 3 Proposition 3 Youtube Proclus (p. 357, 9) explains that euclid uses the word alternate (or, more exactly, alternately, ἐναλλάξ) in two connexions, (1) of a certain transformation of a proportion, as in book v. and the arithmetical books, (2) as here, of certain of the angles formed by parallels with a straight line crossing them. The elements consists of thirteen books. book 1 outlines the fundamental propositions of plane geometry, includ ing the three cases in which triangles are congruent, various theorems involving parallel lines, the theorem regarding the sum of the angles in a triangle, and the pythagorean theorem. book 2 is commonly said to deal with “geometric. The elements (greek: Στοιχεῖα stoikheîa) is a mathematical treatise consisting of 13 books attributed to the ancient greek mathematician euclid c. 300 bc. it is a collection of definitions, postulates, propositions (theorems and constructions), and mathematical proofs of the propositions. the books cover plane and solid euclidean. Proposition 1. to find the centre of a given circle. let abc be the given circle; thus it is required to find the centre of the circle abc. let a straight line ab be drawn. through it at random, and let it be bisected at the point d; from d let dc be drawn at right angles to ab and let it be drawn through to e; let ce be bisected at f; i say.
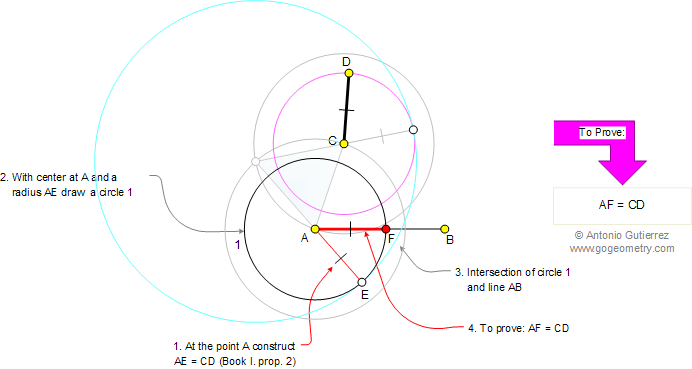
Euclid S Elements Book I Proposition 3 Given Two Unequal Straight The elements (greek: Στοιχεῖα stoikheîa) is a mathematical treatise consisting of 13 books attributed to the ancient greek mathematician euclid c. 300 bc. it is a collection of definitions, postulates, propositions (theorems and constructions), and mathematical proofs of the propositions. the books cover plane and solid euclidean. Proposition 1. to find the centre of a given circle. let abc be the given circle; thus it is required to find the centre of the circle abc. let a straight line ab be drawn. through it at random, and let it be bisected at the point d; from d let dc be drawn at right angles to ab and let it be drawn through to e; let ce be bisected at f; i say. The to take is that there is a lot of material in the book, and it’s not especially easy. book i contains 23 definitions, five postulates, five common notions, and 47 propositions. each proposition includes a proof based on the definitions, postulates, common notions, and earlier propositions. although one could study book i sequentially. Beginning in book xi, solids are considered, and they form the last kind of magnitude discussed in the elements. the propositions following the definitions, postulates, and common notions, there are 48 propositions. each of these propositions includes a statement followed by a proof of the statement.

Euclid Elements I 3 The to take is that there is a lot of material in the book, and it’s not especially easy. book i contains 23 definitions, five postulates, five common notions, and 47 propositions. each proposition includes a proof based on the definitions, postulates, common notions, and earlier propositions. although one could study book i sequentially. Beginning in book xi, solids are considered, and they form the last kind of magnitude discussed in the elements. the propositions following the definitions, postulates, and common notions, there are 48 propositions. each of these propositions includes a statement followed by a proof of the statement.

Comments are closed.