Euclid Elements I 3
Euclid S Elements Book I Proposition 3 Given Two Unequal Straight This edition of euclid’s elements presents the definitive greek text—i.e., that edited by j.l. heiberg (1883– 1885)—accompanied by a modern english translation, as well as a greek english lexicon. neither the spurious books 14 and 15, nor the extensive scholia which have been added to the elements over the centuries, are included. Leon and theudius also wrote versions before euclid (fl. ca. 295 b.c.e.). these other elements have all been lost since euclid’s replaced them. it is conceivable that in some of these earlier versions the construction in proposition i.2 was not known, so this proposition would instead have been a postulate (a stronger version of i.post.3 ).

Euclid S Elements Introduction The elements (greek: Στοιχεῖα stoikheîa) is a mathematical treatise consisting of 13 books attributed to the ancient greek mathematician euclid c. 300 bc. it is a collection of definitions, postulates, propositions (theorems and constructions), and mathematical proofs of the propositions. the books cover plane and solid euclidean. Proclus (p. 357, 9) explains that euclid uses the word alternate (or, more exactly, alternately, ἐναλλάξ) in two connexions, (1) of a certain transformation of a proportion, as in book v. and the arithmetical books, (2) as here, of certain of the angles formed by parallels with a straight line crossing them. A point is that which has no part. definition 2. a line is breadthless length. definition 3. the ends of a line are points. definition 4. a straight line is a line which lies evenly with the points on itself. definition 5. a surface is that which has length and breadth only. Euclid could have chosen proposition i.4 to come first, since it doesn’t logically depend on the previous three, but there are some good reasons for putting i.1 first. for one thing, the elements ends with constructions of the five regular solids in book xiii, so it is a nice aesthetic touch to begin with the construction of a regular triangle.

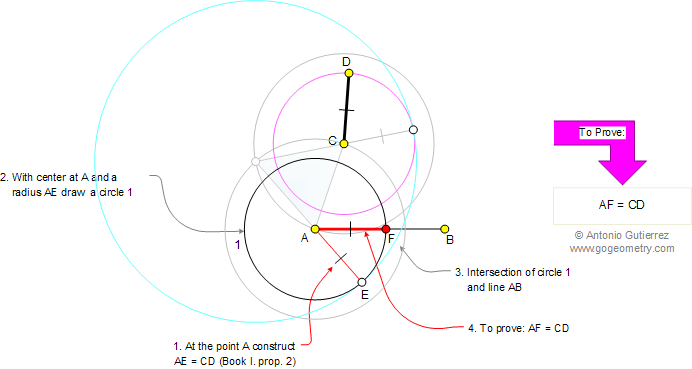
Euclid S Elements Index Online Geometry Tutor Elearning College A point is that which has no part. definition 2. a line is breadthless length. definition 3. the ends of a line are points. definition 4. a straight line is a line which lies evenly with the points on itself. definition 5. a surface is that which has length and breadth only. Euclid could have chosen proposition i.4 to come first, since it doesn’t logically depend on the previous three, but there are some good reasons for putting i.1 first. for one thing, the elements ends with constructions of the five regular solids in book xiii, so it is a nice aesthetic touch to begin with the construction of a regular triangle. Euclid, elements i 3© translated by henry mendell (cal. state u., l.a.) return to vignettes of ancient mathematics return to elements i, introduction go to prop. 2 go to prop. 4. prop. 3: with two given, unequal straight lines to take away from the larger a straight line equal to the smaller. (general diagram). let the given two unequal. This edition of euclid’s elements presents the definitive greek text—i.e., that edited by j.l. heiberg (1883– 1885)—accompanied by a modern english translation, as well as a greek english lexicon. neither the spurious books 14 and 15, nor the extensive scholia which have been added to the elements over the centuries, are included.

Ppt Chapter 1 Euclid S Elements Powerpoint Presentation Free Euclid, elements i 3© translated by henry mendell (cal. state u., l.a.) return to vignettes of ancient mathematics return to elements i, introduction go to prop. 2 go to prop. 4. prop. 3: with two given, unequal straight lines to take away from the larger a straight line equal to the smaller. (general diagram). let the given two unequal. This edition of euclid’s elements presents the definitive greek text—i.e., that edited by j.l. heiberg (1883– 1885)—accompanied by a modern english translation, as well as a greek english lexicon. neither the spurious books 14 and 15, nor the extensive scholia which have been added to the elements over the centuries, are included.

The First Six Books Of The Elements Of Euclid In Which Coloured

Comments are closed.