Esquema Tema 1 Pag 2 Valor Absoluto Matematicas Factores

Esquema Tema 1 Pág 2 Valor Absoluto Matematicas Factores Teoría – tema 1: valor absoluto página 2 7 valor absoluto de un número real el valor absoluto de un número real a se escribe ∣a∣ y es el mismo número a cuando es positivo o cero, y opuesto de a cuando es negativo. se define como: ∣a∣={−a si a<0 a>0 si a≥0} el valor absoluto cumple las siguientes propiedades: ∣a∣=∣−a. Mat i tema 01. reales. tema 1. nÚmeros reales. el conjunto de los números reales, denotado por. (o r), es el campo numérico en el que se realizan la mayoría de los trabajos matemáticos. las operaciones algebraicas (con números, con polinomios, con ecuaciones ) se hacen en r. las operaciones con funciones (límites, continuidad.

Matematicas Valor Absoluto Tema 1. nÚmeros reales. 1. números reales. 2. valor absoluto. 3. intervalos y entornos. extraer e introducir factores en un radical. f) racionalización de. Tema 1 – los números reales – matemáticas i – 1º ba chillerato 4 1.2 – valor absoluto de un nÚmero real definiciÓn el valor absoluto de un número real , a, es el propio número a, si es positivo, o su opuesto, a, si es negativo: | a | = < ≥ a si a 0 a si a 0. El valor absoluto de un número se puede describir como su distancia desde el cero en la recta numérica. por lo tanto, se refiere al número en sí mismo, ignorando su signo. en términos matemáticos, el valor absoluto se denota por dos líneas verticales que rodean el número. por ejemplo, el valor absoluto de 3 se escribe como | 3 | y es. A continuación las principales propiedades del valor absoluto: 1) el valor absoluto de un número siempre es positivo o 0, por lo tanto: │x│≥ 0. 2) el valor absoluto de cero también es cero, es decir │0│ = 0, por lo tanto se puede afirmar que: │x│ = 0, si y solo si x = 0. 3) para todo número x que pertenece al conjunto de los.

Valor Absoluto Ejercicios Resueltos Para Principiantes Youtube El valor absoluto de un número se puede describir como su distancia desde el cero en la recta numérica. por lo tanto, se refiere al número en sí mismo, ignorando su signo. en términos matemáticos, el valor absoluto se denota por dos líneas verticales que rodean el número. por ejemplo, el valor absoluto de 3 se escribe como | 3 | y es. A continuación las principales propiedades del valor absoluto: 1) el valor absoluto de un número siempre es positivo o 0, por lo tanto: │x│≥ 0. 2) el valor absoluto de cero también es cero, es decir │0│ = 0, por lo tanto se puede afirmar que: │x│ = 0, si y solo si x = 0. 3) para todo número x que pertenece al conjunto de los. Paso 1: primero establece la expresión dentro de las barras de valor absoluto igual a cero y resuelve para x. 3 − 2x = 0 x = 3 2. tenga en cuenta que 3 − 2x = 0 en x = 3 2. este es el “valor crítico” para esta expresión. pasos 2 y 3: dibuja una recta numérica y marca este valor crítico en la línea. El valor absoluto en la vida. la matemática esta presente a diario en nuestra vida solo que en muchas de estas ocasiones cuando aplicamos conceptos matemáticos, estos no están expuestos de forma explícita, por ejemplo en las distancias cuando avanzamos de un punto a otro y luego retrocedemos al mismo punto, podríamos concluir que el recorrido es nulo, pero en realidad las distancias son.

3con14 Matemáticas E Valor Absoluto Fórmulas Paso 1: primero establece la expresión dentro de las barras de valor absoluto igual a cero y resuelve para x. 3 − 2x = 0 x = 3 2. tenga en cuenta que 3 − 2x = 0 en x = 3 2. este es el “valor crítico” para esta expresión. pasos 2 y 3: dibuja una recta numérica y marca este valor crítico en la línea. El valor absoluto en la vida. la matemática esta presente a diario en nuestra vida solo que en muchas de estas ocasiones cuando aplicamos conceptos matemáticos, estos no están expuestos de forma explícita, por ejemplo en las distancias cuando avanzamos de un punto a otro y luego retrocedemos al mismo punto, podríamos concluir que el recorrido es nulo, pero en realidad las distancias son.
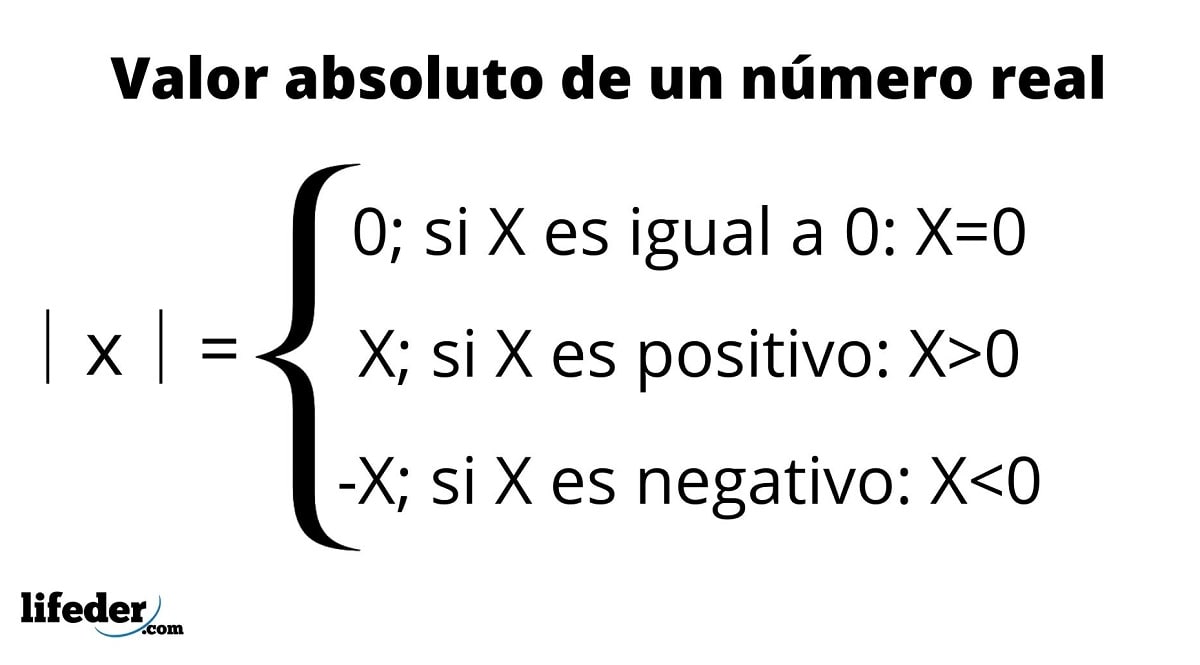
Valor Absoluto Propiedades Ejemplos Ejercicios

Comments are closed.